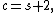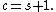“Reeb sphere theorem”的意思、由来-开放百科全书

词条

Reeb sphere theorem

释义

Morse foliation
Reeb sphere theorem
Generalization
References

In mathematics, Reeb sphere theorem, named after Georges Reeb, states that

A closed oriented connected manifold Mⁿ that admits a singular foliation having only centers is homeomorphic to the sphere Sⁿ and the foliation has exactly two singularities.

Morse foliation

A singularity of a foliation F is of Morse type if in its small neighborhood all leaves of the foliation are levels of a Morse function, being the singularity a critical point of the function. The singularity is a center if it is a local extremum of the function; otherwise, the singularity is a saddle.

The number of centers c and the number of saddles , specifically c − s, is tightly connected with the manifold topology.

We denote ind p = min(k, n − k), the index of a singularity , where k is the index of the corresponding critical point of a Morse function. In particular, a center has index 0, index of a saddle is at least 1.

A Morse foliation F on a manifold M is a singular transversely oriented codimension one foliation of class C² with isolated singularities such that:

each singularity of F is of Morse type,
each singular leaf L contains a unique singularity p; in addition, if ind p = 1 then 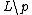is not connected.

Reeb sphere theorem

This is the case c > s = 0, the case without saddles.

Theorem:^[1] Let 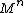be a closed oriented connected manifold of dimension . Assume that 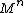admits a -transversely oriented codimension one foliation with a non empty set of singularities all of them centers. Then the singular set of consists of two points and 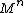is homeomorphic to the sphere .

It is a consequence of the Reeb stability theorem.

Generalization

More general case is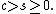

In 1978, E. Wagneur generalized the Reeb sphere theorem to Morse foliations with saddles. He showed that the number of centers cannot be too much as compared with the number of saddles, notably, 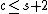. So there are exactly two cases when :

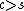(1)

(2)

He obtained a description of the manifold admitting a foliation with singularities that satisfy (1).

Theorem:^[2] Let 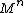be a compact connected manifold admitting a Morse foliation with centers and saddles. Then .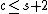

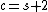In case ,

is homeomorphic to ,
all saddles have index 1,
each regular leaf is diffeomorphic to .

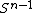Finally, in 2008, C. Camacho and B. Scardua considered the case (2), 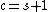. This is possible in a small number of low dimensions.

Theorem:^[3] Let 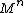be a compact connected manifold and a Morse foliation on . If 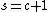, then

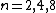or ,
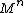is an Eells–Kuiper manifold.

References

1. ^{{citation | last = Reeb | first = Georges | author-link = Georges Reeb | journal = C. R. Acad. Sci. Paris | language = French | mr = 0015613 | pages = 847–849 | title = Sur les points singuliers d'une forme de Pfaff complètement intégrable ou d'une fonction numérique | volume = 222 | year = 1946}}.
2. ^{{citation | last = Wagneur | first = E. | issue = 3 | journal = Annales de l'Institut Fourier | language = French | mr = 511820 | pages = xi, 165–176 | title = Formes de Pfaff à singularités non dégénérées | url = http://www.numdam.org/item?id=AIF_1978__28_3_165_0 | volume = 28 | year = 1978}}.
3. ^{{citation | last1 = Camacho | first1 = César | last2 = Scárdua | first2 = Bruno | arxiv = math/0611395 | doi = 10.1090/S0002-9939-08-09371-4 | issue = 11 | journal = Proceedings of the American Mathematical Society | mr = 2425748 | pages = 4065–4073 | title = On foliations with Morse singularities | volume = 136 | year = 2008}}.

2 : Foliations|Theorems in topology

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。