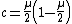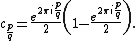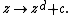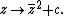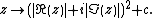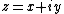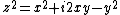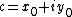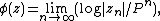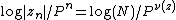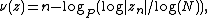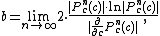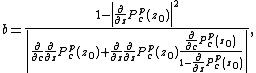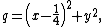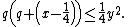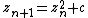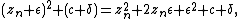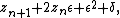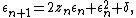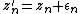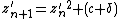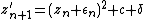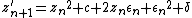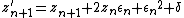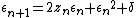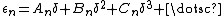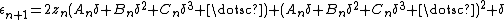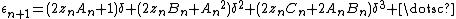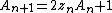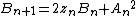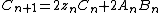- History
- Formal definition
- Basic properties
- Other properties Main cardioid and period bulbs Hyperbolic components Local connectivity Self-similarity Further results Relationship with Julia sets
- Geometry Pi in the Mandelbrot set Fibonacci sequence in the Mandelbrot set Image gallery of a zoom sequence
- Generalizations Multibrot sets Higher dimensions
- Other, non-analytic, mappings
- Computer drawings Escape time algorithm Histogram coloring Continuous (smooth) coloring Distance estimates Exterior distance estimation Interior distance estimation Optimizations Cardioid / bulb checking Periodicity checking Border tracing / edge checking Symmetry utilization Advanced bailout method Perturbation theory and series approximation
- References in popular culture
- See also
- References
- Further reading
- External links
Upon looking at a picture of the Mandelbrot set, one immediately notices the large cardioid-shaped region in the center. This main cardioid
is the region of parameters  for which
for which  has an attracting fixed point. It consists of all parameters of the form
has an attracting fixed point. It consists of all parameters of the form
for some  in the open unit disk.
in the open unit disk.
To the left of the main cardioid, attached to it at the point 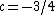 , a circular-shaped bulb is visible. This bulb consists of those parameters
, a circular-shaped bulb is visible. This bulb consists of those parameters  for which
for which  has an attracting cycle of period 2. This set of parameters is an actual circle, namely that of radius 1/4 around −1.
has an attracting cycle of period 2. This set of parameters is an actual circle, namely that of radius 1/4 around −1.
There are infinitely many other bulbs tangent to the main cardioid: for every rational number 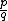 , with p and q coprime, there is such a bulb that is tangent at the parameter
, with p and q coprime, there is such a bulb that is tangent at the parameter
This bulb is called the 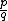 -bulb of the Mandelbrot set. It consists of parameters that have an attracting cycle of period
-bulb of the Mandelbrot set. It consists of parameters that have an attracting cycle of period  and combinatorial rotation number
and combinatorial rotation number 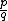 . More precisely, the
. More precisely, the  periodic Fatou components containing the attracting cycle all touch at a common point (commonly called the
periodic Fatou components containing the attracting cycle all touch at a common point (commonly called the  -fixed point). If we label these components
-fixed point). If we label these components 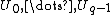 in counterclockwise orientation, then
in counterclockwise orientation, then  maps the component
maps the component  to the component
to the component 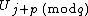 .
.
The change of behavior occurring at 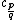 is known as a bifurcation: the attracting fixed point "collides" with a repelling period q-cycle. As we pass through the bifurcation parameter into the
is known as a bifurcation: the attracting fixed point "collides" with a repelling period q-cycle. As we pass through the bifurcation parameter into the 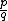 -bulb, the attracting fixed point turns into a repelling fixed point (the
-bulb, the attracting fixed point turns into a repelling fixed point (the  -fixed point), and the period q-cycle becomes attracting.
-fixed point), and the period q-cycle becomes attracting.
Hyperbolic components
All the bulbs we encountered in the previous section were interior components of
the Mandelbrot set in which the maps  have an attracting periodic cycle. Such components are called hyperbolic components.
have an attracting periodic cycle. Such components are called hyperbolic components.
It is conjectured that these are the only interior regions of  . This problem, known as density of hyperbolicity, may be the most important open problem in the field of complex dynamics. Hypothetical non-hyperbolic components of the Mandelbrot set are often referred to as "queer" or ghost components.[17][18]
. This problem, known as density of hyperbolicity, may be the most important open problem in the field of complex dynamics. Hypothetical non-hyperbolic components of the Mandelbrot set are often referred to as "queer" or ghost components.[17][18]
For real quadratic polynomials, this question was answered positively in the 1990s independently by Lyubich and by Graczyk and Świątek. (Note that hyperbolic components intersecting the real axis correspond exactly to periodic windows in the Feigenbaum diagram. So this result states that such windows exist near every parameter in the diagram.)
Not every hyperbolic component can be reached by a sequence of direct bifurcations from the main cardioid of the Mandelbrot set. However, such a component can be reached by a sequence of direct bifurcations from the main cardioid of a little Mandelbrot copy (see below).
Each of the hyperbolic components has a center, which is a point c such that the inner Fatou domain for 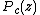 has a super-attracting cycle – that is, that the attraction is infinite (see the image here). This means that the cycle contains the critical point 0, so that 0 is iterated back to itself after some iterations. We therefore have that
has a super-attracting cycle – that is, that the attraction is infinite (see the image here). This means that the cycle contains the critical point 0, so that 0 is iterated back to itself after some iterations. We therefore have that  n
n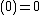 for some n. If we call this polynomial
for some n. If we call this polynomial 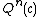 (letting it depend on c instead of z), we have that
(letting it depend on c instead of z), we have that 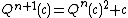 and that the degree of
and that the degree of 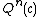 is
is  . We can therefore construct the centers of the hyperbolic components by successively solving the equations
. We can therefore construct the centers of the hyperbolic components by successively solving the equations 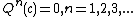 . The number of new centers produced in each step is given by Sloane's {{oeis|A000740}}.
. The number of new centers produced in each step is given by Sloane's {{oeis|A000740}}.
Local connectivity
It is conjectured that the Mandelbrot set is locally connected. This famous conjecture is known as MLC (for Mandelbrot locally connected). By the work of Adrien Douady and John H. Hubbard, this conjecture would result in a simple abstract "pinched disk" model of the Mandelbrot set. In particular, it would imply the important hyperbolicity conjecture mentioned above.
The work of Jean-Christophe Yoccoz established local connectivity of the Mandelbrot set at all finitely renormalizable parameters; that is, roughly speaking those contained only in finitely many small Mandelbrot copies.[19] Since then, local connectivity has been proved at many other points of  , but the full conjecture is still open.
, but the full conjecture is still open.
Self-similarity
The Mandelbrot set in general is not strictly self-similar but it is quasi-self-similar, as small slightly different versions of itself can be found at arbitrarily small scales.
The little copies of the Mandelbrot set are all slightly different, mostly because of the thin threads connecting them to the main body of the set.
Further results
The Hausdorff dimension of the boundary of the Mandelbrot set equals 2 as determined by a result of Mitsuhiro Shishikura.[23] It is not known whether the boundary of the Mandelbrot set has positive planar Lebesgue measure.
In the Blum-Shub-Smale model of real computation, the Mandelbrot set is not computable, but its complement is computably enumerable. However, many simple objects (e.g., the graph of exponentiation) are also not computable in the BSS model. At present, it is unknown whether the Mandelbrot set is computable in models of real computation based on computable analysis, which correspond more closely to the intuitive notion of "plotting the set by a computer". Hertling has shown that the Mandelbrot set is computable in this model if the hyperbolicity conjecture is true.
Relationship with Julia sets
As a consequence of the definition of the Mandelbrot set, there is a close correspondence between the geometry of the Mandelbrot set at a given point and the structure of the corresponding Julia set. For instance, a point is in the Mandelbrot set exactly when the corresponding Julia set is connected.
This principle is exploited in virtually all deep results on the Mandelbrot set. For example, Shishikura proved that, for a dense set of parameters in the boundary of the Mandelbrot set, the Julia set has Hausdorff dimension two, and then transfers this information to the parameter plane.[22] Similarly, Yoccoz first proved the local connectivity of Julia sets, before establishing it for the Mandelbrot set at the corresponding parameters.[19] Adrien Douady phrases this principle as:
{{quote|Plough in the dynamical plane, and harvest in parameter space.}}
Geometry
For every rational number 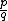 , where p and q are relatively prime, a hyperbolic component of period q bifurcates from the main cardioid. The part of the Mandelbrot set connected to the main cardioid at this bifurcation point is called the p/q-limb. Computer experiments suggest that the diameter of the limb tends to zero like
, where p and q are relatively prime, a hyperbolic component of period q bifurcates from the main cardioid. The part of the Mandelbrot set connected to the main cardioid at this bifurcation point is called the p/q-limb. Computer experiments suggest that the diameter of the limb tends to zero like 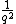 . The best current estimate known is the Yoccoz-inequality, which states that the size tends to zero like
. The best current estimate known is the Yoccoz-inequality, which states that the size tends to zero like 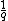 .
.
A period-q limb will have q − 1 "antennae" at the top of its limb. We can thus determine the period of a given bulb by counting these antennas.
Pi in the Mandelbrot set
In an attempt to demonstrate that the thickness of the p/q-limb is zero, David Boll carried out a computer experiment in 1991, where he computed the number of iterations required for the series to diverge for z = 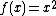 (
(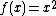 being the location thereof). As the series doesn't diverge for the exact value of z =
being the location thereof). As the series doesn't diverge for the exact value of z = 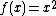 , the number of iterations required increases with a small ε. It turns out that multiplying the value of ε with the number of iterations required yields an approximation of π that becomes better for smaller ε. For example, for ε = 0.0000001 the number of iterations is 31415928 and the product is 3.1415928.[23]
, the number of iterations required increases with a small ε. It turns out that multiplying the value of ε with the number of iterations required yields an approximation of π that becomes better for smaller ε. For example, for ε = 0.0000001 the number of iterations is 31415928 and the product is 3.1415928.[23]
Fibonacci sequence in the Mandelbrot set
It can be shown that the Fibonacci sequence is located within the Mandelbrot Set and that a relation exists between the main cardioid and the Farey Diagram. Upon mapping the main cardioid to a disk, one can notice that the amount of antennae that extends from the next largest Hyperbolic component, and that is located between the two previously selected components, follows suit with the Fibonacci sequence. The amount of antennae also correlates with the Farey Diagram and the denominator amounts within the corresponding fractional values, of which relate to the distance around the disk. Both portions of these fractional values themselves can be summed together after  to produce the location of the next Hyperbolic component within the sequence. Thus, the Fibonacci sequence of 1, 2, 3, 5, 8, 13, and 21 can be found within the Mandelbrot set.
to produce the location of the next Hyperbolic component within the sequence. Thus, the Fibonacci sequence of 1, 2, 3, 5, 8, 13, and 21 can be found within the Mandelbrot set.
Image gallery of a zoom sequence
The Mandelbrot set shows more intricate detail the closer one looks or magnifies the image, usually called "zooming in". The following example of an image sequence zooming to a selected c value gives an impression of the infinite richness of different geometrical structures and explains some of their typical rules.
The magnification of the last image relative to the first one is about 1010 to 1. Relating to an ordinary monitor, it represents a section of a Mandelbrot set with a diameter of 4 million kilometers. Its border would show an astronomical number of different fractal structures.
{{Clear}}The seahorse "body" is composed by 25 "spokes" consisting of two groups of 12 "spokes" each and one "spoke" connecting to the main cardioid. These two groups can be attributed by some kind of metamorphosis to the two "fingers" of the "upper hand" of the Mandelbrot set; therefore, the number of "spokes" increases from one "seahorse" to the next by 2; the "hub" is a so-called Misiurewicz point. Between the "upper part of the body" and the "tail" a distorted small copy of the Mandelbrot set called satellite may be recognized.
| ] | ] |
The islands above seem to consist of infinitely many parts like Cantor sets, as is{{Clarify|date=May 2010}} actually the case for the corresponding Julia set Jc. However, they are connected by tiny structures, so that the whole represents a simply connected set. The tiny structures meet each other at a satellite in the center that is too small to be recognized at this magnification. The value of c for the corresponding Jc is not that of the image center but, relative to the main body of the Mandelbrot set, has the same position as the center of this image relative to the satellite shown in the 6th zoom step.
Generalizations
{{multiple image| image1 = Mandelbrot Set Animation 1280x720.gif
| image2 = Mandelbrot set from powers 0.05 to 2.webm
| width2 = 150
| footer = Animations of the Multibrot set for d from 0 to 5 (left) and from 0.05 to 2 (right).
}}
Multibrot sets
Multibrot sets are bounded sets found in the complex plane for members of the general monic univariate polynomial family of recursions
For an integer d, these sets are connectedness loci for the Julia sets built from the same formula. The full cubic connectedness locus has also been studied; here one considers the two-parameter recursion 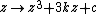 , whose two critical points are the complex square roots of the parameter k. A parameter is in the cubic connectedness locus if both critical points are stable.[24] For general families of holomorphic functions, the boundary of the Mandelbrot set generalizes to the bifurcation locus, which is a natural object to study even when the connectedness locus is not useful.
, whose two critical points are the complex square roots of the parameter k. A parameter is in the cubic connectedness locus if both critical points are stable.[24] For general families of holomorphic functions, the boundary of the Mandelbrot set generalizes to the bifurcation locus, which is a natural object to study even when the connectedness locus is not useful.
The Multibrot set is obtained by varying the value of the exponent d. The article has a video that shows the development from d = 0 to 7, at which point there are 6 i.e. (d − 1) lobes around the perimeter. A similar development with negative exponents results in (1 − d) clefts on the inside of a ring.
Higher dimensions
There is no perfect extension of the Mandelbrot set into 3D. This is because there is no 3D analogue of the complex numbers for it to iterate on. However, there is an extension of the complex numbers into 4 dimensions, called the quaternions, that creates a perfect extension of the Mandelbrot set and the Julia sets into 4 dimensions.[25] These can then be either cross-sectioned or projected into a 3D structure.
Other, non-analytic, mappings
Of particular interest is the tricorn fractal, the connectedness locus of the anti-holomorphic family
The tricorn (also sometimes called the Mandelbar) was encountered by Milnor in his study of parameter slices of real cubic polynomials. It is not locally connected. This property is inherited by the connectedness locus of real cubic polynomials.
Another non-analytic generalization is the Burning Ship fractal, which is obtained by iterating the following :
Computer drawings
]
There are many programs used to generate the Mandelbrot set and other fractals, some of which are described in fractal-generating software. These programs use a variety of algorithms to determine the color of individual pixels and achieve efficient computation.
Escape time algorithm
The simplest algorithm for generating a representation of the Mandelbrot set is known as the "escape time" algorithm. A repeating calculation is performed for each x, y point in the plot area and based on the behavior of that calculation, a color is chosen for that pixel.
The x and y locations of each point are used as starting values in a repeating, or iterating calculation (described in detail below). The result of each iteration is used as the starting values for the next. The values are checked during each iteration to see whether they have reached a critical "escape" condition, or "bailout". If that condition is reached, the calculation is stopped, the pixel is drawn, and the next x, y point is examined. For some starting values, escape occurs quickly, after only a small number of iterations. For starting values very close to but not in the set, it may take hundreds or thousands of iterations to escape. For values within the Mandelbrot set, escape will never occur. The programmer or user must choose how much iteration, or "depth", they wish to examine. The higher the maximal number of iterations, the more detail and subtlety emerge in the final image, but the longer time it will take to calculate the fractal image.
Escape conditions can be simple or complex. Because no complex number with a real or imaginary part greater than 2 can be part of the set, a common bailout is to escape when either coefficient exceeds 2. A more computationally complex method that detects escapes sooner, is to compute distance from the origin using the Pythagorean theorem, i.e., to determine the absolute value, or modulus, of the complex number. If this value exceeds 2, or equivalently, when the sum of the squares of the real and imaginary parts exceed 4, the point has reached escape. More computationally intensive rendering variations include the Buddhabrot method, which finds escaping points and plots their iterated coordinates.
The color of each point represents how quickly the values reached the escape point. Often black is used to show values that fail to escape before the iteration limit, and gradually brighter colors are used for points that escape. This gives a visual representation of how many cycles were required before reaching the escape condition.
To render such an image, the region of the complex plane we are considering is subdivided into a certain number of pixels. To color any such pixel, let  be the midpoint of that pixel. We now iterate the critical point 0 under
be the midpoint of that pixel. We now iterate the critical point 0 under  , checking at each step whether the orbit point has modulus larger than 2. When this is the case, we know that
, checking at each step whether the orbit point has modulus larger than 2. When this is the case, we know that  does not belong to the Mandelbrot set, and we color our pixel according to the number of iterations used to find out. Otherwise, we keep iterating up to a fixed number of steps, after which we decide that our parameter is "probably" in the Mandelbrot set, or at least very close to it, and color the pixel black.
does not belong to the Mandelbrot set, and we color our pixel according to the number of iterations used to find out. Otherwise, we keep iterating up to a fixed number of steps, after which we decide that our parameter is "probably" in the Mandelbrot set, or at least very close to it, and color the pixel black.
In pseudocode, this algorithm would look as follows. The algorithm does not use complex numbers and manually simulates complex-number operations using two real numbers, for those who do not have a complex data type. The program may be simplified if the programming language includes complex-data-type operations.
For each pixel (Px, Py) on the screen, do:{ x0 = scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.5, 1)) y0 = scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1, 1)) x = 0.0 y = 0.0 iteration = 0 max_iteration = 1000 while (x*x + y*y <= 2*2 AND iteration < max_iteration) { xtemp = x*x - y*y + x0 y = 2*x*y + y0 x = xtemp iteration = iteration + 1 } color = palette[iteration] plot(Px, Py, color)}Here, relating the pseudocode to  ,
,  and
and  :
:
and so, as can be seen in the pseudocode in the computation of x and y:
-
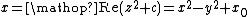 and
and 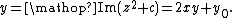
To get colorful images of the set, the assignment of a color to each value of the number of executed iterations can be made using one of a variety of functions (linear, exponential, etc.). One practical way, without slowing down calculations, is to use the number of executed iterations as an entry to a look-up color palette table initialized at startup. If the color table has, for instance, 500 entries, then the color selection is n mod 500, where n is the number of iterations.
Histogram coloring
{{Unreferenced section|date=October 2018}}A more complex coloring method involves using a histogram, which keeps track of how many pixels reached each iteration number, from 1 to n. This method will equally distribute colors to the same overall area, and, importantly, is independent of the maximal number of iterations chosen.
First, create an array of size n. For each pixel, which took i iterations, find the ith element and increment it. This creates the histogram during computation of the image. Then, when finished, perform a second "rendering" pass over each pixel, utilizing the completed histogram. If you had a continuous color palette ranging from 0 to 1, you could find the normalized color of each pixel as follows, using the variables from above.
total = 0
for (i = 0; i < max_iterations; ++i) {
}
hue = 0.0;
for (i = 0; i <= iteration; ++i) {
}
color = palette[hue]
This method may be combined with the smooth coloring method below for more aesthetically pleasing images.
Continuous (smooth) coloring
{{multiple image| direction = vertical| width = 180
| image1 = Escape Time Algorithm bands.png
| caption1 = This image was rendered with the escape time algorithm. There are very obvious "bands" of color
| image2 = Normalized Iteration Count Algorithm 1.png
| caption2 = This image was rendered with the normalized iteration count algorithm. The bands of color have been replaced by a smooth gradient. Also, the colors take on the same pattern that would be observed if the escape time algorithm were used.
}}
The escape time algorithm is popular for its simplicity. However, it creates bands of color, which, as a type of aliasing, can detract from an image's aesthetic value. This can be improved using an algorithm known as "normalized iteration count",[26][27] which provides a smooth transition of colors between iterations. The algorithm associates a real number  with each value of z by using the connection of the iteration number with the potential function. This function is given by
with each value of z by using the connection of the iteration number with the potential function. This function is given by
where zn is the value after n iterations and P is the power for which z is raised to in the Mandelbrot set equation (zn+1 = znP + c, P is generally 2).
If we choose a large bailout radius N (e.g., 10100), we have that
for some real number 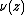 , and this is
, and this is
and as n is the first iteration number such that |zn| > N, the number we subtract from n is in the interval [0, 1).
For the coloring we must have a cyclic scale of colors (constructed mathematically, for instance) and containing H colors numbered from 0 to H − 1 (H = 500, for instance). We multiply the real number 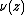 by a fixed real number determining the density of the colors in the picture, take the integral part of this number modulo H, and use it to look up the corresponding color in the color table.
by a fixed real number determining the density of the colors in the picture, take the integral part of this number modulo H, and use it to look up the corresponding color in the color table.
For example, modifying the above pseudocode and also using the concept of linear interpolation would yield
For each pixel (Px, Py) on the screen, do:{ x0 = scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.5, 1)) y0 = scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1, 1)) x = 0.0 y = 0.0 iteration = 0 max_iteration = 1000 // Here N=2^8 is chosen as a reasonable bailout radius. while ( x*x + y*y <= (1 << 16) AND iteration < max_iteration ) { xtemp = x*x - y*y + x0 y = 2*x*y + y0 x = xtemp iteration = iteration + 1 } // Used to avoid floating point issues with points inside the set. if ( iteration < max_iteration ) { // sqrt of inner term removed using log simplification rules. log_zn = log( x*x + y*y ) / 2 nu = log( log_zn / log(2) ) / log(2) // Rearranging the potential function. // Dividing log_zn by log(2) instead of log(N = 1<<8) // because we want the entire palette to range from the // center to radius 2, NOT our bailout radius. iteration = iteration + 1 - nu } color1 = palette[floor(iteration)] color2 = palette[floor(iteration) + 1] // iteration % 1 = fractional part of iteration. color = linear_interpolate(color1, color2, iteration % 1) plot(Px, Py, color)}Distance estimates
One can compute the distance from point c (in exterior or interior) to nearest point on the boundary of the Mandelbrot set.[28]
Exterior distance estimation
The proof of the connectedness of the Mandelbrot set in fact gives a formula for the uniformizing map of the complement of  (and the derivative of this map). By the Koebe quarter theorem, one can then estimate the distance between the midpoint of our pixel and the Mandelbrot set up to a factor of 4.
(and the derivative of this map). By the Koebe quarter theorem, one can then estimate the distance between the midpoint of our pixel and the Mandelbrot set up to a factor of 4.
In other words, provided that the maximal number of iterations is sufficiently high, one obtains a picture of the Mandelbrot set with the following properties:
- Every pixel that contains a point of the Mandelbrot set is colored black.
- Every pixel that is colored black is close to the Mandelbrot set.
The distance estimate b of a pixel c (a complex number) from the Mandelbrot set is given by
where
-
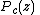 stands for complex quadratic polynomial
stands for complex quadratic polynomial -
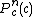 stands for n iterations of
stands for n iterations of 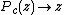 or
or 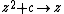 , starting with
, starting with  :
: 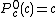 ,
, 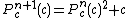 ;
; -
 is the derivative of
is the derivative of 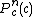 with respect to c. This derivative can be found by starting with
with respect to c. This derivative can be found by starting with 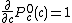 and then
and then 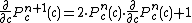 . This can easily be verified by using the chain rule for the derivative.
. This can easily be verified by using the chain rule for the derivative.
The idea behind this formula is simple: When the equipotential lines for the potential function 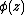 lie close, the number
lie close, the number 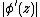 is large, and conversely, therefore the equipotential lines for the function
is large, and conversely, therefore the equipotential lines for the function 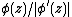 should lie approximately regularly.
should lie approximately regularly.
From a mathematician's point of view, this formula only works in limit where n goes to infinity, but very reasonable estimates can be found with just a few additional iterations after the main loop exits.
Once b is found, by the Koebe 1/4-theorem, we know that there is no point of the Mandelbrot set with distance from c smaller than b/4.
The distance estimation can be used for drawing of the boundary of the Mandelbrot set, see the article Julia set.
Interior distance estimation
It is also possible to estimate the distance of a limitly periodic (i.e., inner) point to the boundary of the Mandelbrot set. The estimate is given by
where
-
 is the period,
is the period, -
 is the point to be estimated,
is the point to be estimated, -
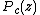 is the complex quadratic polynomial
is the complex quadratic polynomial 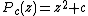
-
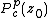 is the
is the  -fold iteration of
-fold iteration of 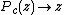 , starting with
, starting with 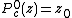
-
 is any of the
is any of the  points that make the attractor of the iterations of
points that make the attractor of the iterations of 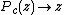 starting with
starting with 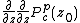 ,
, 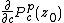 and
and 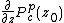 are various derivatives of
are various derivatives of 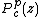 , evaluated at
, evaluated at  .
.
Analogous to the exterior case, once b is found, we know that all points within the distance of b/4 from c are inside the Mandelbrot set.
There are two practical problems with the interior distance estimate: first, we need to find  precisely, and second, we need to find
precisely, and second, we need to find  precisely.
precisely.
The problem with  is that the convergence to
is that the convergence to  by iterating
by iterating 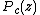 requires, theoretically, an infinite number of operations.
requires, theoretically, an infinite number of operations.
The problem with any given  is that, sometimes, due to rounding errors, a period is falsely identified to be an integer multiple of the real period (e.g., a period of 86 is detected, while the real period is only 43=86/2). In such case, the distance is overestimated, i.e., the reported radius could contain points outside the Mandelbrot set.
is that, sometimes, due to rounding errors, a period is falsely identified to be an integer multiple of the real period (e.g., a period of 86 is detected, while the real period is only 43=86/2). In such case, the distance is overestimated, i.e., the reported radius could contain points outside the Mandelbrot set.
Optimizations
Cardioid / bulb checking
One way to improve calculations is to find out beforehand whether the given point lies within the cardioid or in the period-2 bulb. Before passing the complex value through the escape time algorithm, first check that:
,
,
,
where x represents the real value of the point and y the imaginary value. The first two equations determine that the point is within the cardioid, the last the period-2 bulb.
The cardioid test can equivalently be performed without the square root:
3rd- and higher-order buds do not have equivalent tests, because they are not perfectly circular.[29] However, it is possible to find whether the points are within circles inscribed within these higher-order bulbs, preventing many, though not all, of the points in the bulb from being iterated.
Periodicity checking
To prevent having to do huge numbers of iterations for points in the set, one can perform periodicity checking. Check whether a point reached in iterating a pixel has been reached before. If so, the pixel cannot diverge and must be in the set.
Periodicity checking is, of course, a trade-off. The need to remember points costs memory and data management instructions, whereas it saves computational instructions.
However, checking against only one previous iteration can detect many periods with little performance overhead. For example, within the while loop of the pseudocode above, make the following modifications.
while (x*x + y*y <= 2*2 AND iteration < max_iteration) { xtemp = x*x - y*y + x0 ytemp = 2*x*y + y0 if (x == xtemp AND y == ytemp) { // do not work, because 1) only the body has a cycle period of 1, 2) end cycles will be reached after millions or billions of iterations, 3) rounding errors end up in longer final cycles iteration = max_iteration break } x = xtemp y = ytemp iteration = iteration + 1 }Border tracing / edge checking
It can be shown that if a solid shape can be drawn on the Mandelbrot set, with all the border colors being the same, then the shape can be filled in with that color. This is a result of the Mandelbrot set being simply connected. Boundary tracing works by following the lemniscates of the various iteration levels (colored bands) all around the set, and then filling the entire band at once. This can be a good speed increase, because it means that large numbers of points can be skipped.[30]
A similar method operating on the same principle uses rectangles instead of arbitrary border shapes. It is usually faster than boundary tracing because it requires fewer calculations to work out the rectangle. It is inefficient, however, because boundaries are not rectangular, and so some areas can be missed. This issue can be minimized by creating a recursive algorithm that, if a rectangle border fails, will subdivide it into four smaller rectangles and test those, and either fill each or subdivide again and repeat the process.
However, this only works using discrete colors in the escape time algorithm. It will not work for smooth/continuous coloring.
Symmetry utilization
The horizontal symmetry of the Mandelbrot set allows for portions of the rendering process to be skipped upon the presence of the real axis in the final image. However, regardless of the portion that gets mirrored, the same number of points will be rendered.
Advanced bailout method
Simple programs and scripts generally tend to set the escape value to two. This process can be improved by utilizing the distance from the origin and the point being rendered with the Pythagorean theorem by summing the squares of the real and imaginary portions of  and then escaping if the value is larger or equal to four. The result of this optimization is a faster rendering of the image.
and then escaping if the value is larger or equal to four. The result of this optimization is a faster rendering of the image.
Perturbation theory and series approximation
Very highly magnified images require more than the standard 64–128 or so bits of precision that most hardware floating-point units provide, requiring renderers to use slow "bignum" or "arbitrary-precision" math libraries to calculate. However, this can be sped up by the exploitation of perturbation theory. Given
as the iteration, and a small epsilon and delta, it is the case that
or
so if one defines
one can calculate a single point (e.g. the center of an image) using high-precision arithmetic (z), giving a reference orbit, and then compute many points around it in terms of various initial offsets delta plus the above iteration for epsilon, where epsilon-zero is set to 0. For most iterations, epsilon does not need more than 16 significant figures, and consequently hardware floating-point may be used to get a mostly accurate image.[31] There will often be some areas where the orbits of points diverge enough from the reference orbit that extra precision is needed on those points, or else additional local high-precision-calculated reference orbits are needed. By measuring the orbit distance between the reference point and the point calculated with low precision, it can be detected that it is not possible to calculate the point correctly, and the calculation can be stopped. These incorrect points can later be re-calculated e.g. from another closer reference point.
Further, it is possible to approximate the starting values for the low-precision points with a truncated Taylor series, which often enables a significant amount of iterations to be skipped.[32]
Renderers implementing these techniques are publicly available and offer speedups for highly magnified images by around two orders of magnitude.[33]
An alternate explanation of the above:
For the central point in the disc  and its iterations
and its iterations  , and an arbitrary point in the disc
, and an arbitrary point in the disc  and its iterations
and its iterations 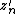 , it is possible to define the following iterative relationship:
, it is possible to define the following iterative relationship:
With 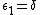 . Successive iterations of
. Successive iterations of  can be found using the following:
can be found using the following:
Now from the original definition:
,
It follows that:
As the iterative relationship relates an arbitrary point to the central point by a very small change  , then most of the iterations of
, then most of the iterations of  are also small and can be calculated using floating point hardware.
are also small and can be calculated using floating point hardware.
However, for every arbitrary point in the disc it is possible to calculate a value for a given 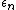 without having to iterate through the sequence from
without having to iterate through the sequence from  , by expressing
, by expressing  as a power series of
as a power series of  .
.
With 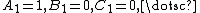 .
.
Now given the iteration equation of  , it is possible to calculate the coefficients of the power series for each
, it is possible to calculate the coefficients of the power series for each  :
:
Therefore it follows that:
The coefficents in the power series can be calculated as iterative series using only values from the central point's iterations  , and do not change for any arbitrary point in the disc. If
, and do not change for any arbitrary point in the disc. If  is very small,
is very small,  should be calculable to sufficient accuracy using only a few terms of the power series. As the Mandelbrot Escape Contours are 'continuous' over the complex plane, if a points escape time has been calculated, then the escape time of that points neighbours should be similar. Interpolation of the neighbouring points should provide a good estimation of where to start in the
should be calculable to sufficient accuracy using only a few terms of the power series. As the Mandelbrot Escape Contours are 'continuous' over the complex plane, if a points escape time has been calculated, then the escape time of that points neighbours should be similar. Interpolation of the neighbouring points should provide a good estimation of where to start in the  series.
series.
Further, separate interpolation of both real axis points and imaginary axis points should provide both an upper and lower bound for the point being calculated. If both results are the same (i.e. both escape or dot not escape) then the difference  can be used to recuse until both an upper and lower bound can be established. If floating point hardware can be used to iterate the
can be used to recuse until both an upper and lower bound can be established. If floating point hardware can be used to iterate the  series, then there exists a relation between how many iterations can be achieved in the time it takes to use BigNum software to compute a given
series, then there exists a relation between how many iterations can be achieved in the time it takes to use BigNum software to compute a given  . If the difference between the bounds is greater than the number of iterations, it is possible to perform binomial search using BigNum software, successively halving the gap until it becomes more time efficient to find the escape value using floating point hardware.
. If the difference between the bounds is greater than the number of iterations, it is possible to perform binomial search using BigNum software, successively halving the gap until it becomes more time efficient to find the escape value using floating point hardware.
References in popular culture
The Mandelbrot set is considered by many the most popular fractal,[34][35] and has been such referenced several times in popular culture.
- The Jonathan Coulton song "Mandelbrot Set" is a tribute to both the fractal itself and to its father Benoit Mandelbrot.[36]
- The second book of the Mode series by Piers Anthony, Fractal Mode, describes a world that is a perfect 3D model of the set.[37]
- The Arthur C. Clarke novel The Ghost from the Grand Banks features an artificial lake made to replicate the shape of the Mandelbrot set.[38]
- The South Korean heavy metal singer Norazo made a music video Ni pal za ya (your fortune), which starts with hypnotic video including Mandelbrot set.[39]
- The album Jupiters Darling by American rock band Heart prominently features a Mandelbrot set on the cover. The set is rotated so that the cusp is on the top, resembling a heart.
- In the second episode (The Big Bran Hypothesis) of the television series ‘’The Big Bang Theory’’, Leonard says that Penny’s apartment is a little messy. Sheldon fires back with “The Mandelbrot set of complex numbers is a little messy. This is chaos.”
- In the movie Matrix Revolutions, the opening scene is depicting the matrix code to consist out of infinitely regressing information, featuring a Mandelbrot set.
See also
{{Portal|Geometry}}- Collatz fractal
- Fractint
- Gilbreath permutation
- Mandelbox
- Mandelbulb
- Newton fractal
- Orbit portrait
- Orbit trap
- Pickover stalk
References
2. ^Robert Brooks and Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in {{cite book|author=Irwin Kra|editor=Irwin Kra|others=Bernard Maskit|title=Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference|url=https://books.google.com/books?id=eTzSSu0LH7kC&pg=65--71|date=1 May 1981|publisher=Princeton University Press|isbn=0-691-08267-7|pages=65–71}}
3. ^{{cite web |url=http://sprott.physics.wisc.edu/pubs/paper311.pdf |title=Biophilic Fractals and the Visual Journey of Organic Screen-savers |author=R.P. Taylor & J.C. Sprott |accessdate=1 January 2009 |format=pdf |year=2008 |work=Nonlinear Dynamics, Psychology, and Life Sciences, Vol. 12, No. 1 |publisher=Society for Chaos Theory in Psychology & Life Sciences }}
4. ^Benoit Mandelbrot, Fractal aspects of the iteration of
 for complex
for complex 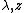 , Annals of the New York Academy of Sciences 357, 249/259
, Annals of the New York Academy of Sciences 357, 249/2595. ^{{cite book |title=The Beauty of Fractals |last=Peitgen |first=Heinz-Otto |authorlink= |author2=Richter Peter |year=1986 |publisher=Springer-Verlag |location=Heidelberg |isbn=0-387-15851-0 |pages= }}
6. ^Frontiers of Chaos, Exhibition of the Goethe-Institut by H.O. Peitgen, P. Richter, H. Jürgens, M. Prüfer, D.Saupe. since 1985 shown in over 40 countries.
7. ^{{cite book |title=Making a New Science |last=Gleick |first=James |authorlink= |year=1987 |publisher=Cardinal |location=London |isbn= |pages=229 }}
8. ^{{cite book |title=A computer microscope zooms in for a close look at the most complicated object in mathematics |last=Dewdney |first=A. K. |authorlink= |year=1985 |publisher=Scientific American |location=http://www.nature.com/scientificamerican/journal/v253/n2/pdf/scientificamerican0885-16.pdf |pages=16–24}} {{subscription required}}
9. ^{{cite book |title=Fractals: The Patterns of Chaos |author=John Briggs |year=1992 |page=80}}
10. ^{{cite magazine |last=Pountain |first=Dick |date=September 1986 |title=Turbocharging Mandelbrot |url=https://archive.org/stream/byte-magazine-1986-09/1986_09_BYTE_11-09_The_68000_Family#page/n370/mode/1up |magazine=Byte |access-date=11 November 2015 }}
11. ^{{cite journal | author = Lyubich, Mikhail | title = Six Lectures on Real and Complex Dynamics | version = | publisher = | date = May–June 1999 | url = http://citeseer.ist.psu.edu/cache/papers/cs/28564/http:zSzzSzwww.math.sunysb.eduzSz~mlyubichzSzlectures.pdf/ | format = | accessdate = 2007-04-04 }}
12. ^{{cite journal | last = Lyubich | first = Mikhail | authorlink = Mikhail Lyubich | title = Regular and stochastic dynamics in the real quadratic family | journal = Proceedings of the National Academy of Sciences of the United States of America | volume = 95 | issue =24 | pages = 14025–14027 | publisher = | date=November 1998 | url = http://www.pnas.org/cgi/reprint/95/24/14025.pdf | format=PDF| doi = 10.1073/pnas.95.24.14025 | id = | accessdate = 2007-04-04 | pmid = 9826646 | pmc = 24319 | bibcode =1998PNAS...9514025L }}
13. ^{{cite web|url=http://math.bu.edu/DYSYS/explorer/def.html|title=Mandelbrot Set Explorer: Mathematical Glossary|accessdate=2007-10-07}}
14. ^{{cite web|url=http://mrob.com/pub/muency/escaperadius.html|title=Escape Radius, Mu-Ency at MROB|accessdate=2015-10-21}}
15. ^{{Cite web|url=http://www.math.brown.edu/~kahn/mconn.pdf|title=The Mandelbrot Set is Connected: a Topological Proof|last=Kahn|first=Jeremy|date=8 August 2001|website=|archive-url=|archive-date=|dead-url=|access-date=}}
16. ^The Mandelbrot set, theme and variations. Tan, Lei. Cambridge University Press, 2000. {{isbn|978-0-521-77476-5}}. Section 2.1, "Yoccoz para-puzzles", [https://books.google.com/books?id=-a_DsYXquVkC&pg=PA121 p. 121]
17. ^Exploring the Mandelbrot set. The Orsay Notes by Adrien Douady and John H. Hubbard. page 12
18. ^Wolf Jung, March 2002, Homeomorphisms on Edges of the Mandelbrot Set by Wolf Jung
19. ^1 {{citation | last = Hubbard | first = J. H. | contribution = Local connectivity of Julia sets and bifurcation loci: three theorems of J.-C. Yoccoz | contribution-url = http://www.math.cornell.edu/~hubbard/hubbard.pdf | location = Houston, TX | mr = 1215974 | pages = 467–511 | publisher = Publish or Perish | title = Topological methods in modern mathematics (Stony Brook, NY, 1991) | year = 1993}}. Hubbard cites as his source a 1989 unpublished manuscript of Yoccoz.
20. ^{{cite journal | last1 = Lei | first1 = | year = 1990 | title = Similarity between the Mandelbrot set and Julia Sets | url = http://projecteuclid.org/euclid.cmp/1104201823| journal = Communications in Mathematical Physics | volume = 134 | issue = | pages = 587–617 | doi=10.1007/bf02098448| bibcode = 1990CMaPh.134..587L}}
21. ^{{cite book |author=J. Milnor |chapter=Self-Similarity and Hairiness in the Mandelbrot Set |editor=M. C. Tangora |location=New York |pages=211–257 |title=Computers in Geometry and Topology |url=https://books.google.com/books?id=wuVJAQAAIAAJ |year=1989|publisher=Taylor & Francis}})
22. ^1 {{citation | last = Shishikura | first = Mitsuhiro | arxiv = math.DS/9201282 | doi = 10.2307/121009 | issue = 2 | journal = Annals of Mathematics | mr = 1626737 | pages = 225–267 | series = Second Series | title = The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets | volume = 147 | year = 1998}}.
23. ^Gary William Flake, The Computational Beauty of Nature, 1998. p. 125. {{isbn|978-0-262-56127-3}}.
24. ^Rudy Rucker's discussion of the CCM: CS.sjsu.edu
25. ^http://archive.bridgesmathart.org/2010/bridges2010-247.pdf retrieved August 19 2018
26. ^{{cite journal|last=García|first=Francisco|author2=Ángel Fernández |author3=Javier Barrallo |author4=Luis Martín |title=Coloring Dynamical Systems in the Complex Plane|url=http://math.unipa.it/~grim/Jbarrallo.PDF|format=PDF|accessdate=2008-01-21}}
27. ^{{cite web|url=http://linas.org/art-gallery/escape/escape.html|title=Renormalizing the Mandelbrot Escape|author=Linas Vepstas}}
28. ^{{cite web | url=http://www.moleculardensity.net/buddhabrot/appendix/2 | title=Interior and exterior distance bounds for the Mandelbrot | author=Albert Lobo Cusidó}}
29. ^{{cite web|url=http://linas.org/art-gallery/bud/bud.html|title=Mandelbrot Bud Maths}}
30. ^{{cite web|url=http://www.reocities.com/CapeCanaveral/5003/mandel.htm|title=Boundary Tracing Method|archiveurl=https://web.archive.org/web/20150220012221/http://www.reocities.com/CapeCanaveral/5003/mandel.htm|archivedate=2015-02-20}}
31. ^{{cite web|url=http://www.fractalforums.com/announcements-and-news/superfractalthing-arbitrary-precision-mandelbrot-set-rendering-in-java/|title=Superfractalthing - Arbitrary Precision Mandelbrot Set Rendering in Java}}
32. ^{{cite journal|author=K. I. Martin|url=http://www.superfractalthing.co.nf/sft_maths.pdf|title=Superfractalthing Maths}}
33. ^{{cite web|url=http://www.chillheimer.de/kallesfraktaler/|title=Kalles Fraktaler 2}}
34. ^Mandelbaum, Ryan F. (2018). [https://gizmodo.com/this-trippy-music-video-is-made-of-3d-fractals-1822168809 "This Trippy Music Video Is Made of 3D Fractals."] Retrieved 17 January, 2019
35. ^Moeller, Olga de. (2018).[https://thewest.com.au/lifestyle/kids/what-are-fractals-ng-b88838072z "what are Fratals?"] Retrieved 17 January, 2019.
36. ^{{cite web|title=Mandelbrot Set|url=http://www.jonathancoulton.com/wiki/Mandelbrot_Set|website=JoCopeda|accessdate=15 January 2015}}
37. ^{{cite book|author=Piers Anthony|title=Fractal Mode|url=https://books.google.com/books?id=XdUyAAAACAAJ|year=1992|publisher=HarperCollins|isbn=978-0-246-13902-3}}
38. ^{{cite book|author=Arthur C. Clarke|title=The Ghost From The Grand Banks|url=https://books.google.com/books?id=6ELsYigmXNoC|date=29 September 2011|publisher=Orion|isbn=978-0-575-12179-9}}
39. ^{{cite web |format=video |url=https://www.youtube.com/watch?v=s0UjELAUMjE |title=NORAZO "니팔자야" 역대최강 M/V / Ni pal ja ya (your fortune) |website=YouTube |others=Published in February 22, 2015 by NORAZO PRODUCTION}}
Further reading
- John W. Milnor, Dynamics in One Complex Variable (Third Edition), Annals of Mathematics Studies 160, (Princeton University Press, 2006), {{isbn|0-691-12488-4}}
(First appeared in 1990 as a [https://web.archive.org/web/20060424085751/http://www.math.sunysb.edu/preprints.html Stony Brook IMS Preprint], available as arXiV:math.DS/9201272 ) - Nigel Lesmoir-Gordon, The Colours of Infinity: The Beauty, The Power and the Sense of Fractals, {{isbn|1-904555-05-5}}
(includes a DVD featuring Arthur C. Clarke and David Gilmour) - Heinz-Otto Peitgen, Hartmut Jürgens, Dietmar Saupe, Chaos and Fractals: New Frontiers of Science (Springer, New York, 1992, 2004), {{isbn|0-387-20229-3}}
External links
{{Wikibooks|Fractals }}{{commons}}- {{dmoz|Science/Math/Chaos_and_Fractals|Chaos and Fractals}}
- The Mandelbrot Set and Julia Sets by Michael Frame, Benoit Mandelbrot, and Nial Neger
- Video: Mandelbrot fractal zoom to 6.066 e228
- मण्डलबेथ (maṇḍalabeth) 3D analog of the mandelbrot set, with various symmetry groups
- [https://www.youtube.com/watch?v=NGMRB4O922I Relatively simple explanation of the mathematical process, by Dr Holly Krieger, MIT]
- Mandelbrot set images online rendering
- [https://github.com/pkulchenko/ZeroBraneEduPack/blob/master/fractal-samples/zplane.lua Fractal calculator written in Lua by Deyan Dobromiroiv, Sofia, Bulgaria]
- Global Arabic Encyclopedia
- Global Assessment of Function
- Global Awards
- Global Banking and Finance Review (Magazine)
- Global Banking & Finance Awards
- Global Banking & Finance Review (Magazine)
- Global Bioenergies
- Global Boxing Council
- Global Boxing Union
- Global Brokerage
- Global burden of disease
- Global Burden of Diseases, Injuries, and Risk Factors Study
- Global Burden of Diseases, Injuries, and Risk Factors Study 2015
- Global Business School Barcelona
- Global business track
- Global caliphate
- Global carbon dioxide
- Global Cash Access
- Global Catastrophic Risks
- Global Catastrophic Risks (book)
- Global Catholic Network
- Global Catholic Television
- Global Cebu F.C.
- Global Center to Combat Extremism
- Global Centre for Combating Extremist Ideology