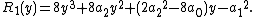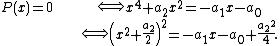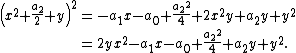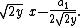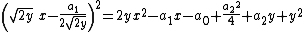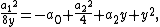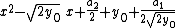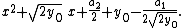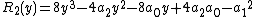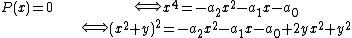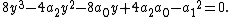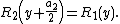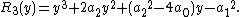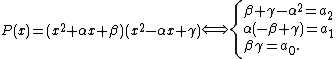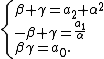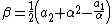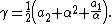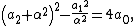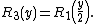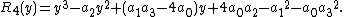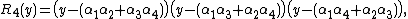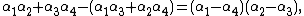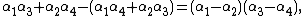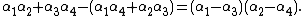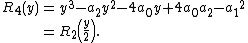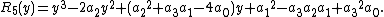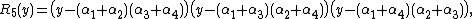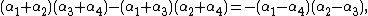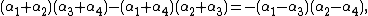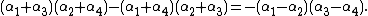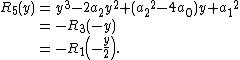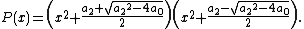1. Definitions
    First definition  Second definition  Third definition  Fourth definition  Fifth definition 

2. Applications
    Solving quartic equations  Factoring quartic polynomials  Galois groups of irreducible quartic polynomials 

3. See also

4. References

In algebra, a resolvent cubic is one of several distinct, although related, cubic polynomials defined from a monic polynomial of degree four:

In each case:

• The coefficients of the resolvent cubic can be obtained from the coefficients of {{math|P(x)}} using only sums, subtractions and multiplications.
• Knowing the roots of the resolvent cubic of {{math|P(x)}} is useful for finding the roots of {{math|P(x)}} itself. Hence the name “resolvent cubic”.
• The polynomial {{math|P(x)}} has a multiple root if and only if its resolvent cubic has a multiple root.

Definitions

Suppose that the coefficients of {{math|P(x)}} belong to a field {{math|k}} whose characteristic is different from {{math|2}}. In other words, we are working in a field in which {{math|1 + 1 ≠ 0}}. Whenever roots of {{math|P(x)}} are mentioned, they belong to some extension {{math|K}} of {{math|k}} such that {{math|P(x)}} factors into linear factors in {{math|K[x]}}. If {{math|k}} is the field {{math|Q}} of rational numbers, then {{mvar|K}} can be the field {{math|C}} of complex numbers or the field {{overline|{{math|Q}}}} of algebraic numbers.

In some cases, the concept of resolvent cubic is defined only when {{math|P(x)}} is a quartic in depressed form—that is, when {{math|a₃ {{=}} 0}}.

Note that the fourth and fifth definitions below also make sense and that the relationship between these resolvent cubics and {{math|P(x)}} are still valid if the characteristic of {{mvar|k}} is equal to {{math|2}}.

First definition

Suppose that {{math|P(x)}} is a depressed quartic—that is, that {{math|a₃ {{=}} 0}}. A possible definition of the resolvent cubic of {{math|P(x)}} is:^[1]

The origin of this definition lies in applying Ferrari's method to find the roots of {{math|P(x)}}. To be more precise:

Add a new unknown, {{mvar|y}}, to {{math|x² + a₂/2}}. Now you have:

If this expression is a square, it can only be the square of

But the equality

is equivalent to

and this is the same thing as the assertion that {{math|R₁(y)}} = 0.

If {{math|y₀}} is a root of {{math|R₁(y)}}, then it is a consequence of the computations made above that the roots of {{math|P(x)}} are the roots of the polynomial

together with the roots of the polynomial

Of course, this makes no sense if {{math|y₀ {{=}} 0}}, but since the constant term of {{math|R₁(y)}} is {{math|–a₁²}}, {{math|0}} is a root of {{math|R₁(y)}} if and only if {{math|a₁ {{=}} 0}}, and in this case the roots of {{math|P(x)}} can be found using the quadratic formula.

Second definition

Another possible definition^[1] (still supposing that {{math|P(x)}} is a depressed quartic) is

The origin of this definition is similar to the previous one. This time, we start by doing:

and a computation similar to the previous one shows that this last expression is a square if and only if

A simple computation shows that

Third definition

Another possible definition^[2][3] (again, supposing that {{math|P(x)}} is a depressed quartic) is

The origin of this definition lies in another method of solving quartic equations, namely Descartes' method. If you try to find the roots of {{math|P(x)}} by expressing it as a product of two monic quadratic polynomials {{math|x² + αx + β}} and {{math|x² – αx + γ}}, then

If there is a solution of this system with {{math|α ≠ 0}} (note that if {{math|a₁ ≠ 0}}, then this is automatically true for any solution), the previous system is equivalent to

It is a consequence of the first two equations that then

and

After replacing, in the third equation, {{math|β}} and {{math|γ}} by these values one gets that

and this is equivalent to the assertion that {{math|α²}} is a root of {{math|R₃(y)}}. So, again, knowing the roots of {{math|R₃(y)}} helps to determine the roots of {{math|P(x)}}.

Note that

Fourth definition

Still another possible definition is^[4]

In fact, if the roots of {{math|P(x)}} are {{math|α₁, α₂, α₃}}, and {{math|α₄}}, then

a fact the follows from Vieta's formulas. In other words, R₄(y) is the monic polynomial whose roots are

It is easy to see that

and

Therefore, {{math|P(x)}} has a multiple root if and only if {{math|R₄(y)}} has a multiple root. More precisely, {{math|P(x)}} and {{math|R₄(y)}} have the same discriminant.

One should note that if {{math|P(x)}} is a depressed polynomial, then

Fifth definition

Yet another definition is^[5][6]

If, as above, the roots of {{math|P(x)}} are {{math|α₁, α₂, α₃}}, and {{math|α₄}}, then

again as a consequence of Vieta's formulas. In other words, {{math|R₅(y)}} is the monic polynomial whose roots are

It is easy to see that

and

Therefore, as it happens with {{math|R₄(y)}}, {{math|P(x)}} has a multiple root if and only if {{math|R₅(y)}} has a multiple root. More precisely, {{math|P(x)}} and {{math|R₅(y)}} have the same discriminant. This is also a consequence of the fact that {{math|R₅(y + a₂)}} = {{math|R₄(y)}}.

Note that if {{math|P(x)}} is a depressed polynomial, then

Applications

Solving quartic equations

It was explained above how {{math|R₁(y)}}, {{math|R₂(y)}}, and {{math|R₃(y)}} can be used to find the roots of {{math|P(x)}} if this polynomial is depressed. In the general case, one simply has to find the roots of the depressed polynomial {{math|P(x − a₃/4)}}. For each root {{math|x₀}} of this polynomial, {{math|x₀ − a₃/4}} is a root of {{math|P(x)}}.

Factoring quartic polynomials

If a quartic polynomial {{math|P(x)}} is reducible in {{math|k[x]}}, then it is the product of two quadratic polynomials or the product of a linear polynomial by a cubic polynomial. This second possibility occurs if and only if {{math|P(x)}} has a root in {{math|k}}. In order to determine whether or not {{math|P(x)}} can be expressed as the product of two quadratic polynomials, let us assume, for simplicity, that {{math|P(x)}} is a depressed polynomial. Then it was seen above that if the resolvent cubic {{math|R₃(y)}} has a non-null root of the form {{math|α²}}, for some {{math|α ∈ k}}, then such a decomposition exists.

This can be used to prove that, in {{math|R[x]}}, every quartic polynomial without real roots can be expressed as the product of two quadratic polynomials. Let {{math|P(x)}} be such a polynomial. We can assume without loss of generality that {{math|P(x)}} is monic. We can also assume without loss of generality that it is a reduced polynomial, because {{math|P(x)}} can be expressed as the product of two quadratic polynomials if and only if {{math|P(x − a₃/4)}} can and this polynomial is a reduced one. Then {{math|R₃(y)}} = {{math|y³ + 2a₂y² + (a₂² − 4a₀)y − a₁²}}. There are two cases:

• If {{math|a₁ ≠ 0}} then {{math|R₃(0)}} = {{math|−a₁² < 0}}. Since {{math|R₃(y) > 0}} if {{math|y}} is large enough, then, by the intermediate value theorem, {{math|R₃(y)}} has a root {{math|y₀}} with {{math|y₀ > 0}}. So, we can take {{math|α}} = {{math|{{sqrt|y₀}}}}.
• If {{math|a₁}} = {{math|0}}, then {{math|R₃(y)}} = {{math|y³ + 2a₂y² + (a₂² − 4a₀)y}}. The roots of this polynomial are {{math|0}} and the roots of the quadratic polynomial {{math|y² + 2a₂y + a₂² − 4a₀}}. If {{math|a₂² − 4a₀ < 0}}, then the product of the two roots of this polynomial is smaller than {{math|0}} and therefore it has a root greater than {{math|0}} (which happens to be {{math|−a₂ + 2{{sqrt|a₀}}}}) and we can take {{math|α}} as the square root of that root. Otherwise, {{math|a₂² − 4a₀ ≥ 0}} and then,

More generally, if {{math|k}} is a real closed field, then every quartic polynomial without roots in {{math|k}} can be expressed as the product of two quadratic polynomials in {{math|k[x]}}. Indeed, this statement can be expressed in first-order logic and any such statement that holds for {{math|R}} also holds for any real closed field.

A similar approach can be used to get an algorithm^[2] to determine whether or not a quartic polynomial {{math|P(x) ∈ Q[x]}} is reducible and, if it is, how to express it as a product of polynomials of smaller degree. Again, we will suppose that {{math|P(x)}} is monic and depressed. Then {{math|P(x)}} is reducible if and only if at least one of the following conditions holds:

• The polynomial {{math|P(x)}} has a rational root (this can be determined using the rational root theorem).
• The resolvent cubic {{math|R₃(y)}} has a root of the form {{math|α²}}, for some non-null rational number {{math|α}} (again, this can be determined using the rational root theorem).
• The number {{math|a₂² − 4a₀}} is the square of a rational number and {{math|a₁}} = {{math|0}}.

Indeed:

• If {{math|P(x)}} has a rational root {{math|r}}, then {{math|P(x)}} is the product of {{math|x − r}} by a cubic polynomial in {{math|Q[x]}}, which can be determined by polynomial long division or by Ruffini's rule.
• If there is a rational number {{math|α ≠ 0}} such that {{math|α²}} is a root of {{math|R₃(y)}}, it was shown above how to express {{math|P(x)}} as the product of two quadratic polynomials in {{math|Q[x]}}.
• Finally, if the third condition holds and if {{math|δ ∈ Q}} is such that {{math|δ² }}={{math| a₂² − 4a₀}}, then {{math|P(x)}} = {{math|(x² + (a₂ + δ)/2)(x² + (a₂ − δ)/2)}}.

Galois groups of irreducible quartic polynomials

The resolvent cubic of an irreducible quartic polynomial {{math|P(x)}} can be used to determine its Galois group {{math|G}}; that is, the Galois group of the splitting field of {{math|P(x)}}. Let {{mvar|m}} be the degree over {{mvar|k}} of the splitting field of the resolvent cubic (it can be either {{math|R₄(y)}} or {{math|R₅(y)}}; they have the same splitting field). Then the group {{mvar|G}} is a subgroup of the symmetric group {{math|S₄}}. More precisely:^[4]

• If {{math|m {{=}} 1}} (that is, if the resolvent cubic factors into linear factors in {{mvar|k}}), then {{mvar|G}} is the group {{math|{e, (12)(34), (13)(24), (14)(23)}}}.
• If {{math|m {{=}} 2}} (that is, if the resolvent cubic has one and, up to multiplicity, only one root in {{math|k}}), then, in order to determine {{mvar|G}}, one can determine whether or not {{math|P(x)}} is still irreducible after adjoining to the field {{mvar|k}} the roots of the resolvent cubic. If not, then {{mvar|G}} is a cyclic group of order 4; more precisely, it is one of the three cyclic subgroups of {{math|S₄}} generated by any of its six {{math|4}}-cycles. If it is still irreducible, then {{mvar|G}} is one of the three subgroups of {{math|S₄}} of order {{math|8}}, each of which is isomorphic to the dihedral group of order {{math|8}}.
• If {{math|m {{=}} 3}}, then {{mvar|G}} is the alternating group {{math|A₄}}.
• If {{math|m {{=}} 6}}, then {{mvar|G}} is the whole group {{math|S₄}}.

See also

• Resolvent (Galois theory)

References

• Otoshibe Station
• Otoshidama
• Otoshimono
• Otoshimono (song)
• Otoshi Station
• Otoshop 7.
• Oto Skrbek
• Otospermophilus
• Otospermophilus atricapillus
• Otospermophilus beecheyi
• Otospermophilus variegatus
• Otospermum
• Oto Station
• Otostylis
• Otothyris juquiae
• Otothyris lophophanes
• Otothyris rostrata
• Otothyris travassosi
• Ototo
• Ototo (2010 film)
• Ototo (film)
• Ototoxins
• Otouphepus
• OT: Our Town
• Otou Skrbek