“Ring of mixed characteristic”的意思、由来-开放百科全书

In commutative algebra, a ring of mixed characteristic is a commutative ring

having characteristic zero and having an ideal

such that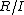

has positive characteristic.^[1]

Examples

The integers

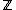have characteristic zero, but for any prime number

is a finite field with

elements and hence has characteristic

The ring of integers of any number field is of mixed characteristic

Fix a prime p and localize the integers at the prime ideal (p). The resulting ring Z_(p) has characteristic zero. It has a unique maximal ideal pZ_(p), and the quotient Z_(p)/pZ_(p) is a finite field with p elements. In contrast to the previous example, the only possible characteristics for rings of the form {{nowrap|Z_(p) / I}} are zero (when I is the zero ideal) and powers of p (when I is any other non-unit ideal); it is not possible to have a quotient of any other characteristic.

is a non-zero prime ideal of the ring

of integers of a number field

then the localization of

is likewise of mixed characteristic.

The p-adic integers Z_p for any prime p are a ring of characteristic zero. However, they have an ideal generated by the image of the prime number p under the canonical map {{nowrap|Z → Z_p}}. The quotient Z_p/pZ_p is again the finite field of p elements. Z_p is an example of a complete discrete valuation ring of mixed characteristic.

The integers, the ring of integers of any number field, and any localization or completion of one of these rings is a characteristic zero Dedekind domain.

References

1. ^{{citation | last1 = Bergman | first1 = George M. | author1-link = George Bergman | last2 = Hausknecht | first2 = Adam O. | doi = 10.1090/surv/045 | isbn = 0-8218-0495-2 | mr = 1387111 | page = 336 | publisher = American Mathematical Society, Providence, RI | series = Mathematical Surveys and Monographs | title = Co-groups and co-rings in categories of associative rings | url = https://books.google.com/books?id=s6NnkQs3JBMC&pg=PA336 | volume = 45 | year = 1996}}.

1 : Commutative algebra