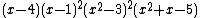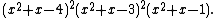“Robertson graph”的意思、由来-开放百科全书

词条

Robertson graph

释义

Algebraic properties
Gallery
References

{{infobox graph
| name = Robertson graph
| image =
| image_caption = The Robertson graph is Hamiltonian.
| namesake = Neil Robertson
| vertices = 19
| edges = 38
| automorphisms = 24 (D₁₂)
| girth = 5
| diameter = 3
| radius = 3
| chromatic_number = 3
| chromatic_index = 5^[1]
| properties = Cage
Hamiltonian
|book thickness=3|queue number=2}}

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.^[2]^[3]

The Robertson graph is the unique (4,5)-cage graph and was discovered by Robertson in 1964.^[4] As a cage graph, it is the smallest 4-regular graph with girth 5.

It has chromatic number 3, chromatic index 5, diameter 3, radius 3 and is both 4-vertex-connected and 4-edge-connected. It has book thickness 3 and queue number 2.^[5]

The Robertson graph is also a Hamiltonian graph which possesses {{formatnum:5376}} distinct directed Hamiltonian cycles.

Algebraic properties

The Robertson graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 24, the group of symmetries of a regular dodecagon, including both rotations and reflections.^[6]

The characteristic polynomial of the Robertson graph is

Gallery

References

1. ^{{MathWorld|urlname=Class2Graph|title=Class 2 Graph}}
2. ^{{MathWorld|urlname=RobertsonGraph|title=Robertson Graph}}
3. ^Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
4. ^Robertson, N. "The Smallest Graph of Girth 5 and Valency 4." Bull. Amer. Math. Soc. 70, 824-825, 1964.
5. ^Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
6. ^Geoffrey Exoo & Robert Jajcay, Dynamic cage survey, Electr. J. Combin. 15, 2008.

2 : Individual graphs|Regular graphs

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。