“Rotation map”的意思、由来-开放百科全书

词条

Rotation map

释义

Definition
Basic properties
Special cases and properties
See also
References

In mathematics, a rotation map is a function that represents an undirected edge-labeled graph, where each vertex enumerates its outgoing neighbors. Rotation maps were first introduced by Reingold, Vadhan and Wigderson (“Entropy waves, the zig-zag graph product, and new constant-degree expanders”, 2002) in order to conveniently define the zig-zag product and prove its properties.

Given a vertex and an edge label , the rotation map returns the 'th neighbor of and the edge label that would lead back to .

Definition

For a D-regular graph G, the rotation map 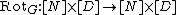is defined as follows: 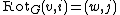if the i th edge leaving v leads to w, and the j th edge leaving w leads to v.

Basic properties

From the definition we see that 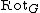is a permutation, and moreover 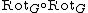is the identity map ( 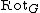is an involution).

Special cases and properties

A rotation map is consistently labeled if all of the edges leaving each vertex are labeled in such a way that at each vertex, the labels of the incoming edges are all distinct. Every regular graph has some consistent labeling.
A rotation map is -consistent if 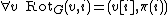. From the definition, a -consistent rotation map is consistently labeled.

References

{{Citation

| first1=O. | last1=Reingold
| first2=S. | last2=Vadhan
| first3=A. | last3=Widgerson
| title=Entropy waves, the zig-zag graph product, and new constant-degree expanders and extractors
| journal=41st Annual Symposium on Foundations of Computer Science
| year=2000
| doi=10.1109/SFCS.2000.892006
| pages=3–13
| arxiv=math/0406038| isbn=978-0-7695-0850-4
}}

{{Citation

| first=O
| last=Reingold
| title=Undirected connectivity in log-space
| journal=Journal of the ACM
| year=2008
| volume=55
| issue=4
| pages=1–24
| doi=10.1145/1391289.1391291
}}

{{Citation

| first1=O. | last1=Reingold
| first2=L. | last2=Trevisan
| first3=S. | last3=Vadhan
| title=Pseudorandom walks on regular digraphs and the RL vs. L problem
| journal=Proceedings of the Thirty-eighth Annual ACM Symposium on Theory of Computing
| year=2006
| doi=10.1145/1132516.1132583
| pages=457
| isbn=978-1595931344
}}{{Refend}}

2 : Extensions and generalizations of graphs|Graph operations

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Basic properties

Special cases and properties

See also

References