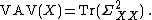“RV coefficient”的意思、由来-开放百科全书

is a multivariate generalization of the squared Pearson correlation coefficient (because the RV coefficient takes values between 0 and 1).^[2]

It measures the closeness of two set of points that may each be represented in a matrix.

The major approaches within statistical multivariate data analysis can all be brought into a common framework in which the RV coefficient is maximised subject to relevant constraints. Specifically, these statistical methodologies include:^[1]

One application of the RV coefficient is in functional neuroimaging where it can measure

Definitions

concerning the definition of scalar-valued quantities which are called the "variance" and "covariance" of vector-valued random variables. Note that standard usage is to have matrices for the variances and covariances of vector random variables.

Given these innovative definitions, the RV-coefficient is then just the correlation coefficient defined in the usual way.

Suppose that X and Y are matrices of centered random vectors (column vectors) with covariance matrix given by

With these definitions, the variance and covariance have certain additive properties in relation to the formation of new vector quantities by extending an existing vector with the elements of another.^[5]

See also

References

1. ^¹{{Cite journal | author1 = Robert, P. | author2 = Escoufier, Y. | title = A Unifying Tool for Linear Multivariate Statistical Methods: The RV-Coefficient | journal = Applied Statistics | year = 1976 | volume = 25 | issue = 3 | pages = 257–265 | doi = 10.2307/2347233 | jstor=2347233}}
2. ^{{Cite book | last = Abdi | first = Hervé | title = RV coefficient and congruence coefficient | publisher = Thousand Oaks | year = 2007 |editor1-first= Neil J |editor1-last= Salkind | isbn = 978-1-4129-1611-0}}
3. ^{{Cite journal | title = Group analysis in functional neuroimaging: selecting subjects using similarity measures | author1 = Ferath Kherif | author2 = Jean-Baptiste Poline | author3 = Sébastien Mériaux | author4 = Habib Banali | author5 = Guillaume Plandin | author6 = Matthew Brett | journal = NeuroImage | volume = 20 | issue = 4 | year = 2003 | pages = 2197–2208 | doi = 10.1016/j.neuroimage.2003.08.018 | pmid=14683722}}
4. ^{{Cite journal | title = How to compute reliability estimates and display confidence and tolerance intervals for pattern classiffers using the Bootstrap and 3-way multidimensional scaling (DISTATIS) | author1 = Herve Abdi | author2 = Joseph P. Dunlop | author3 = Lynne J. Williams | journal = NeuroImage | volume = 45 | year = 2009 | pages = 89–95 | doi = 10.1016/j.neuroimage.2008.11.008 | pmid = 19084072 | issue = 1}}
5. ^¹²³{{Cite journal | author1 = Escoufier, Y. | title = Le Traitement des Variables Vectorielles | journal = Biometrics | year = 1973 | volume = 29 | issue = 4 | pages = 751–760 | doi = 10.2307/2529140 | publisher = International Biometric Society | jstor = 2529140 }}