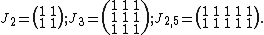1. Properties

2. Applications

3. References

In mathematics, a matrix of ones or all-ones matrix is a matrix where every element is equal to one.^[1] Examples of standard notation are given below:

Some sources call the all-ones matrix the unit matrix,^[2] but that term may also refer to the identity matrix, a different matrix.

Properties

For an {{math|n × n}} matrix of ones J, the following properties hold:

• The trace of J is n,^[3] and the determinant is 1 if n is 1, or 0 otherwise.
• The characteristic polynomial of J is .
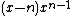• The rank of J is 1 and the eigenvalues are n with multiplicity 1 and 0 with multiplicity {{math|n − 1}}.^[4]
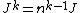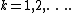• for ^[5]
• J is the neutral element of the Hadamard product.^[6]

When J is considered as a matrix over the real numbers, the following additional properties hold:

• J is positive semi-definite matrix.
• The matrix 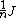is idempotent.^[5]
• The matrix exponential of J is

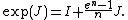
Applications

The all-ones matrix arises in the mathematical field of combinatorics, particularly involving the application of algebraic methods to graph theory. For example, if A is the adjacency matrix of a n-vertex undirected graph G, and J is the all-ones matrix of the same dimension, then G is a regular graph if and only if AJ = JA.^[7] As a second example, the matrix appears in some linear-algebraic proofs of Cayley's formula, which gives the number of spanning trees of a complete graph, using the matrix tree theorem.

References

• Kahramanmarasspor
• Kahramanmaras Sutcu Imam University
• Kahramanmaraş Sütçüimam University
• Kahran
• Kahranmanmaraş
• Kahr Arms P380
• Kahr Arms P-380
• Kahrila-Mustahamba
• Kahri, Polva County
• Kahrizak detention center
• Kahrizli
• Kahrizoba
• Kahr K series
• Kahror Pacca Tehsil
• Kahr P380
• Kahr P-380
• Kahr PM series
• Kahr P Series
• KAHS
• KAHS (disambiguation)
• KAHS-FM
• Kahshe lake
• KAHS-LP
• Kahta
• Kahte Hain Mujhko Raja