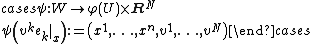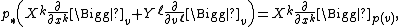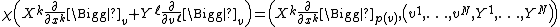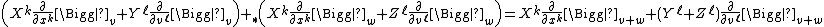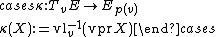“Secondary vector bundle structure”的意思、由来-开放百科全书

词条

Secondary vector bundle structure

释义

Construction of the secondary vector bundle structure
Proof
Linearity of connections on vector bundles
See also
References

In mathematics, particularly differential topology, the secondary vector bundle structure

refers to the natural vector bundle structure {{math|(TE, p_∗, TM)}} on the total space TE of the tangent bundle of a smooth vector bundle {{math|(E, p, M)}}, induced by the push-forward {{math|p_∗ : TE → TM}} of the original projection map {{math|p : E → M}}.

This gives rise to a double vector bundle structure {{math|(TE,E,TM,M)}}.

In the special case {{math|(E, p, M) {{=}} (TM, π_TM, M)}}, where {{math|TE {{=}} TTM}} is the double tangent bundle, the secondary vector bundle {{math|(TTM, (π_TM)_∗, TM)}} is isomorphic to the tangent bundle

{{math|(TTM, π_TTM, TM)}} of {{math|TM}} through the canonical flip.

Construction of the secondary vector bundle structure

Let {{math|(E, p, M)}} be a smooth vector bundle of rank {{mvar|N}}. Then the preimage {{math|(p_∗)⁻¹(X) ⊂ TE}} of any tangent vector {{mvar|X}} in {{math|TM}} in the push-forward {{math|p_∗ : TE → TM}} of the canonical projection {{math|p : E → M}} is a smooth submanifold of dimension {{math|2N}}, and it becomes a vector space with the push-forwards

of the original addition and scalar multiplication

as its vector space operations. The triple {{math|(TE, p_∗, TM)}} becomes a smooth vector bundle with these vector space operations on its fibres.

Proof

Let {{math|(U, φ)}} be a local coordinate system on the base manifold {{mvar|M}} with {{math|φ(x) {{=}} (x¹, ..., xⁿ)}} and let

be a coordinate system on adapted to it. Then

so the fiber of the secondary vector bundle structure at {{mvar|X}} in {{math|T_xM}} is of the form

Now it turns out that

gives a local trivialization {{math|χ : TW → TU × R^2N}} for {{math|(TE, p_∗, TM)}}, and the push-forwards of the original vector space operations read in the adapted coordinates as

and

so each fibre {{math|(p_∗)⁻¹(X) ⊂ TE}} is a vector space and the triple {{math|(TE, p_∗, TM)}} is a smooth vector bundle.

Linearity of connections on vector bundles

The general Ehresmann connection {{math|TE {{=}} HE ⊕ VE}} on a vector bundle {{math|(E, p, M)}} can be characterized in terms of the connector map

where {{math|vl_v : E → V_vE}} is the vertical lift, and {{math|vpr_v : T_vE → V_vE}} is the vertical projection. The mapping

induced by an Ehresmann connection is a covariant derivative on {{math|Γ(E)}} in the sense that

if and only if the connector map is linear with respect to the secondary vector bundle structure {{math|(TE, p_∗, TM)}} on {{math|TE}}. Then the connection is called linear. Note that the connector map is automatically linear with respect to the tangent bundle structure {{math|(TE, π_TE, E)}}.

References

P.Michor. Topics in Differential Geometry, American Mathematical Society (2008).

3 : Differential geometry|Topology|Differential topology

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Construction of the secondary vector bundle structure

Proof

Linearity of connections on vector bundles

See also

References