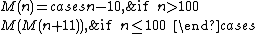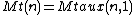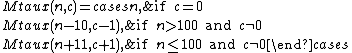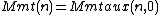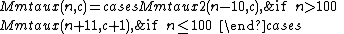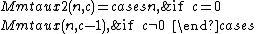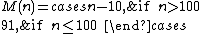“McCarthy 91 function”的意思、由来-开放百科全书

词条

McCarthy 91 function

释义

History
Examples
Code
Proof
Knuth's generalization
References

The McCarthy 91 function is a recursive function, defined by the computer scientist John McCarthy as a test case for formal verification within computer science.

The McCarthy 91 function is defined as

The results of evaluating the function are given by M(n) = 91 for all integer arguments n ≤ 100, and M(n) = n − 10 for n > 100. Indeed, the result of M(101) is also 91 (101 - 10 = 91). All results of M(n) after n = 101 are continually increasing by 1, e.g. M(102) = 92, M(103) = 93.

History

The 91 function was introduced in papers published by Zohar Manna, Amir Pnueli and John McCarthy in 1970. These papers represented early developments towards the application of formal methods to program verification. The 91 function was chosen for being nested-recursive (contrasted with single recursion, such as defining by means of 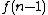). The example was popularized by Manna's book, Mathematical Theory of Computation (1974). As the field of Formal Methods advanced, this example appeared repeatedly in the research literature.

In particular, it is viewed as a "challenge problem" for automated program verification.

It is easier to reason about tail-recursive control flow, this is an equivalent (extensionally equal) definition:

As one of the examples used to demonstrate such reasoning, Manna's book includes a tail-recursive algorithm equivalent to the nested-recursive 91 function. Many of the papers that report an "automated verification" (or termination proof) of the 91 function only handle the tail-recursive version.

This is an equivalent mutually tail-recursive definition:

A formal derivation of the mutually tail-recursive version from the nested-recursive one was given in a 1980 article by Mitchell Wand, based on the use of continuations.

Examples

Example A:

 M(99) = M(M(110)) since 99 ≤ 100       = M(100)    since 110 > 100       = M(M(111)) since 100 ≤ 100       = M(101)    since 111 > 100       = 91        since 101 > 100

Example B:

 M(87) = M(M(98))       = M(M(M(109)))       = M(M(99))       = M(M(M(110)))       = M(M(100))       = M(M(M(111)))       = M(M(101))       = M(91)       = M(M(102))       = M(92)       = M(M(103))       = M(93)    .... Pattern continues increasing till M(99), M(100) and M(101), exactly as we saw on the example A)       = M(101)    since 111 > 100       = 91        since 101 > 100

Code

Here is an implementation of the nested-recursive algorithm in Lisp:

 (defun mc91 (n)   (cond ((<= n 100) (mc91 (mc91 (+ n 11))))         (t (- n 10))))

Here is an implementation of the nested-recursive algorithm in Haskell:

| n > 100 = n - 10
| otherwise = mc91 $ mc91 $ n + 11

Here is an implementation of the nested-recursive algorithm in OCaml:

  let rec mc91 n =    if n > 100 then n - 10    else mc91 (mc91 (n + 11))

Here is an implementation of the tail-recursive algorithm in OCaml:

  let mc91 n =    let rec aux n c =      if c = 0 then n      else if n > 100 then aux (n - 10) (c - 1)      else aux (n + 11) (c + 1)    in    aux n 1

Here is an implementation of the nested-recursive algorithm in Python:

 def mc91(n):    if n > 100:        return n - 10    else:        return mc91(mc91(n + 11))

Here is an implementation of the nested-recursive algorithm in C:

 int mc91(int n) {     if( n > 100 ) {         return n - 10;     } else {         return mc91(mc91(n+11));     } }

Here is an implementation of the tail-recursive algorithm in C:

 int mc91(int n) {     mc91taux(n, 1); }

 int mc91taux(int n, int c) {     if( c != 0 ) {         if( n > 100 ) {             return mc91taux(n - 10, c - 1);         } else {             return mc91taux(n + 11, c + 1);         }     } else {         return n;     } }

Proof

Here is a proof that the function is equivalent to non-recursive:

For 90 ≤ n < 101,

 M(n) = M(M(n + 11))      = M(n + 11 - 10), where n + 11 >= 101 since n >= 90      = M(n + 1)

So M(n) = 91 for 90 ≤ n < 101.

We can use this as a base case for induction on blocks of 11 numbers, like so:

Assume that M(n) = 91 for a ≤ n < a + 11.

Then, for any n such that a - 11 ≤ n < a,

 M(n) = M(M(n + 11))      = M(91), by hypothesis, since a ≤ n + 11 < a + 11      = 91, by the base case.

Now by induction M(n) = 91 for any n in such a block. There are no holes between the blocks, so M(n) = 91 for n < 101. We can also add n = 101 as a special case.

Knuth's generalization

Donald Knuth generalized the 91 function to include additional parameters. John Cowles developed a formal proof that Knuth's generalized function was total, using the ACL2 theorem prover.

References

{{cite journal | author=Zohar Manna and Amir Pnueli | title=Formalization of Properties of Functional Programs | journal=Journal of the ACM |date=July 1970 | volume=17 | issue=3 | pages=555–569 | doi=10.1145/321592.321606}}
{{cite journal | author=Zohar Manna and John McCarthy | title=Properties of programs and partial function logic | journal=Machine Intelligence | year=1970 | volume=5 }}
Zohar Manna. Mathematical Theory of Computation. McGraw-Hill Book Company, New-York, 1974. Reprinted in 2003 by Dover Publications.
{{cite journal | author=Mitchell Wand | title=Continuation-Based Program Transformation Strategies | journal=Journal of the ACM |date=January 1980 | volume=27 | issue=1 | pages=164–180 | doi=10.1145/322169.322183}}
{{cite journal | author = Donald E. Knuth | title = Textbook Examples of Recursion | year = 1991 | journal = Artificial intelligence and mathematical theory of computation | arxiv = cs/9301113| bibcode = 1993cs........1113K }}
{{cite book | author = John Cowles | chapter = Knuth's generalization of McCarthy's 91 function

| title = Computer-Aided reasoning: ACL2 case studies | publisher = Kluwer Academic Publishers
| year = 2000 | pages = 283–299 | url = http://www.cs.utexas.edu/users/moore/acl2/workshop-1999/Cowles-abstract.html}}{{John McCarthy navbox}}

2 : Formal methods|Recurrence relations

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。