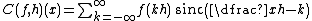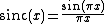“Sinc numerical methods”的意思、由来-开放百科全书

词条

Sinc numerical methods

释义

Sinc numerical methods cover
Reading
References

In numerical analysis and applied mathematics, sinc numerical methods are numerical techniques^[1] for finding approximate solutions of partial differential equations and integral equations based on the translates of sinc function and Cardinal function C(f,h) which is an expansion of f defined by

where the step size h>0 and where the sinc function is defined by

Sinc approximation methods excel for problems whose solutions may have singularities, or infinite domains, or boundary layers.

The truncated Sinc expansion of f is defined by the following series:

.

Sinc numerical methods cover

function approximation,
approximation of derivatives,
approximate definite and indefinite integration,
approximate solution of initial and boundary value ordinary differential equation (ODE) problems,
approximation and inversion of Fourier and Laplace transforms,
approximation of Hilbert transforms,
approximation of definite and indefinite convolution,
approximate solution of partial differential equations,
approximate solution of integral equations,
construction of conformal maps.

Indeed, Sinc are ubiquitous for approximating every operation of calculus

In the standard setup of the sinc numerical methods, the errors (in big O notation) are known to be 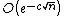with some c>0, where n is the number of nodes or bases used in the methods. However, Sugihara^[2] has recently found that the errors in the Sinc numerical methods based on double exponential transformation are 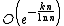with some k>0, in a setup that is also meaningful both theoretically and practically and are found to be best possible in a certain mathematical sense.

Reading

{{cite book

|title=

Handbook of Sinc Numerical Methods

|last1=Stenger |first1=Frank |authorlink1=
|coauthors=
|editor1-last= |editor1-first= |editor1-link=
|year= 2011
|publisher=CRC Press
|location=Boca Raton, Florida
|isbn=9781439821596
|url=
|page=
|pages=
|ref=
}}

{{cite book

|title=Sinc Methods for Quadrature and Differential Equations
|last1=Lund |first1=John |authorlink1=
|last2=Bowers | first2=Kenneth
|coauthors=
|editor1-last= |editor1-first= |editor1-link=
|year= 1992
|publisher=Society for Industrial and Applied Mathematics (SIAM)
|location=Philadelphia
|isbn=9780898712988
|url=
|page=
|pages=
|ref=
}}

References

1. ^{{Cite journal | last1 = Stenger | first1 = F. | doi = 10.1016/S0377-0427(00)00348-4 | title = Summary of sinc numerical methods | journal = Journal of Computational and Applied Mathematics | volume = 121 | pages = 379–420 | year = 2000 | pmid = | pmc = }}
2. ^{{Cite journal | last1 = Sugihara | first1 = M. | last2 = Matsuo | first2 = T. | doi = 10.1016/j.cam.2003.09.016 | title = Recent developments of the Sinc numerical methods | journal = Journal of Computational and Applied Mathematics | volume = 164-165 | pages = 673 | year = 2004 | pmid = | pmc = }}

1 : Numerical analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。