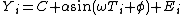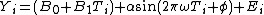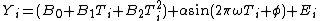“Sinusoidal model”的意思、由来-开放百科全书

词条

Sinusoidal model

释义

Good starting value for C
Good starting value for frequency
Good starting values for amplitude
Model validation
Extensions
See also
References
External links

In statistics, signal processing, and time series analysis, a sinusoidal model to approximate a sequence Y_i is:

where C is constant defining a mean level, α is an amplitude for the sine wave, ω is the frequency, T_i is a time variable, φ is the phase, and E_i is the error sequence in approximating the sequence Y_i by the model. This sinusoidal model can be fit using nonlinear least squares; to obtain a good fit, nonlinear least squares routines may require good starting values for the constant, the amplitude, and the frequency.

Fitting a model with a single sinusoid is a special case of least-squares spectral analysis.

Good starting value for C

A good starting value for C can be obtained by calculating the mean of the data. If the data show a trend, i.e., the assumption of constant location is violated, one can replace C with a linear or quadratic least squares fit. That is, the model becomes

Good starting value for frequency

The starting value for the frequency can be obtained from the dominant frequency in a periodogram. A complex demodulation phase plot can be used to refine this initial estimate for the frequency.{{Fact|date=February 2008}}

Good starting values for amplitude

The root mean square of the detrended data can be scaled by the square root of two to obtain an estimate of the sinusoid amplitude. A complex demodulation amplitude plot can be used to find a good starting value for the amplitude. In addition, this plot can indicate whether or not the amplitude is constant over the entire range of the data or if it varies. If the plot is essentially flat, i.e., zero slope, then it is reasonable to assume a constant amplitude in the non-linear model. However, if the slope varies over the range of the plot, one may need to adjust the model to be:

That is, one may replace α with a function of time. A linear fit is specified in the model above, but this can be replaced with a more elaborate function if needed.

Model validation

As with any statistical model, the fit should be subjected to graphical and quantitative techniques of model validation. For example, a run sequence plot to check for significant shifts in location, scale, start-up effects and outliers. A lag plot can be used to verify the residuals are independent. The outliers also appear in the lag plot, and a histogram and normal probability plot to check for skewness or other non-normality in the residuals.

Extensions

A different method consists in transforming the non-linear regression to a linear regression thanks to a convenient integral equation. Then, there is no need for initial guess and no need for iterative process : the fitting is directly obtained.^[1]

References

1. ^The method is explained in the chapter "Generalized sinusoidal regression" pp.54-63 in the paper:

External links

Beam deflection case study

2 : Regression with time series structure|Regression models

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。