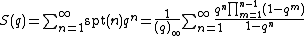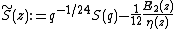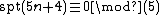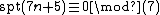“Spt function”的意思、由来-开放百科全书

词条

Spt function

释义

Example
Properties
References

The spt function (smallest parts function) is a function in number theory that counts the sum of the number of smallest parts in each partition of a positive integer. It is related to the partition function.

The first few values of spt(n) are:

1, 3, 5, 10, 14, 26, 35, 57, 80, 119, 161, 238, 315, 440, 589 ... {{OEIS|id=A092269}}

Example

For example, there are five partitions of 4 (with smallest parts underlined):

{{underline|4}}

3 + {{underline|1}}

{{underline|2}} + {{underline|2}}

2 + {{underline|1}} + {{underline|1}}

{{underline|1}} + {{underline|1}} + {{underline|1}} + {{underline|1}}

These partitions have 1, 1, 2, 1, and 4 smallest parts, respectively. So spt(4) = 1 + 1 + 2 + 1 + 4 = 9.

Properties

Like the partition function, spt(n) has a generating function. It is given by

where .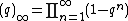

The function is related to a mock modular form. Let 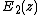denote the weight 2 quasi-modular Eisenstein series and let 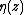denote the Dedekind eta function. Then for 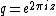, the function

is a mock modular form of weight 3/2 on the full modular group 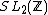with multiplier system 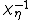, where 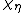is the multiplier system for .

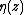While a closed formula is not known for spt(n), there are Ramanujan-like congruences including

^[2]

References

1. ^{{cite journal | title = Congruences for Andrews’ spt-function modulo 32760 and extension of Atkin's Hecke-type partition congruences | author = Frank Garvan}}
2. ^{{cite journal | title = The number of smallest parts in the partitions of n | author = George Andrews }}

2 : Combinatorics|Integer sequences

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。