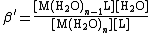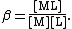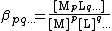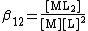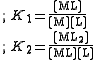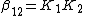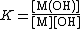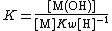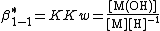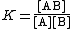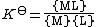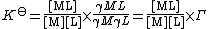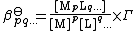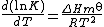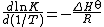- History
- Theory Stepwise and cumulative constants Hydrolysis products Acid–base complexes
- Thermodynamics Ionic strength dependence Temperature dependence
- Factors affecting the stability constants of complexes The chelate effect Deprotonation of aliphatic –OH groups The macrocyclic effect Geometrical factors Classification of metal ions Effect of ionic radius
- Applications Supramolecular complexes
- Experimental methods
- Critically evaluated data
- Databases
- References
- Further reading
- External links
A stability constant (formation constant, binding constant) is an equilibrium constant for the formation of a complex in solution. It is a measure of the strength of the interaction between the reagents that come together to form the complex. There are two main kinds of complex: compounds formed by the interaction of a metal ion with a ligand and supramolecular complexes, such as host–guest complexes and complexes of anions. The stability constant(s) provide the information required to calculate the concentration(s) of the complex(es) in solution. There are many areas of application in chemistry, biology and medicine.
History
Jannik Bjerrum developed the first general method for the determination of stability constants of metal-ammine complexes in 1941.[1] The reasons why this occurred at such a late date, nearly 50 years after Alfred Werner had proposed the correct structures for coordination complexes, have been summarised by Beck and Nagypál.[2] The key to Bjerrum's method was the use of the then recently developed glass electrode and pH meter to determine the concentration of hydrogen ions in solution. Bjerrum recognised that the formation of a metal complex with a ligand was a kind of acid–base equilibrium: there is competition for the ligand, L, between the metal ion, Mn+, and the hydrogen ion, H+. This means that there are two simultaneous equilibria that have to be considered. In what follows electrical charges are omitted for the sake of generality. The two equilibria are
H + L {{eqm}} HL
M + L {{eqm}} ML
Hence by following the hydrogen ion concentration during a titration of a mixture of M and HL with base, and knowing the acid dissociation constant of HL, the stability constant for the formation of ML could be determined. Bjerrum went on to determine the stability constants for systems in which many complexes may be formed.
M + q L {{eqm}} MLq
The following twenty years saw a veritable explosion in the number of stability constants that were determined. Relationships, such as the Irving-Williams series were discovered. The calculations were done by hand using the so-called graphical methods. The mathematics underlying the methods used in this period are summarised by Rossotti and Rossotti.[3] The next key development was the use of a computer program, LETAGROP[4][5] to do the calculations. This permitted the examination of systems too complicated to be evaluated by means of hand-calculations. Subsequently, computer programs capable of handling complex equilibria in general, such as SCOGS[6] and MINIQUAD[7] were developed so that today the determination of stability constants has almost become a "routine" operation. Values of thousands of stability constants can be found in two commercial databases.[8][9]
Theory
The formation of a complex between a metal ion, M, and a ligand, L, is in fact usually a substitution reaction. For example, in aqueous solutions, metal ions will be present as aquo ions, so the reaction for the formation of the first complex could be written as
[M(H2O)n] + L {{eqm}} [M(H2O)n−1L] + H2O
The equilibrium constant for this reaction is given by
[L] should be read as "the concentration of L" and likewise for the other terms in square brackets. The expression can be greatly simplified by removing those terms which are constant. The number of water molecules attached to each metal ion is constant. In dilute solutions the concentration of water is effectively constant. The expression becomes
Following this simplification a general definition can be given, For the general equilibrium
p M + q L … {{eqm}} MpLq…
The definition can easily be extended to include any number of reagents. The reagents need not always be a metal and a ligand but can be any species which form a complex. Stability constants defined in this way, are association constants. This can lead to some confusion as pKa values are dissociation constants. In general purpose computer programs it is customary to define all constants as association constants. The relationship between the two types of constant is given in association and dissociation constants.
Stepwise and cumulative constants
A cumulative or overall constant, given the symbol β, is the constant for the formation of a complex from reagents. For example, the cumulative constant for the formation of ML2 is given by
{M} + 2L <=> ML2 ;{{spaces|5}}
The stepwise constants, K1 and K2 refer to the formation of the complexes one step at a time.
It follows that
A cumulative constant can always be expressed as the product of stepwise constants. Conversely, any stepwise constant can be expressed as a quotient of two or more overall constants. There is no agreed notation for stepwise constants, though a symbol such as K{{su|b=ML|p=L}} is sometimes found in the literature. It is best always to define each stability constant by reference to an equilibrium expression.
Hydrolysis products
The formation of a hydroxo complex is a typical example of a hydrolysis reaction. A hydrolysis reaction is one in which a substrate reacts with water, splitting a water molecule into hydroxide and hydrogen ions. In this case the hydroxide ion then forms a complex with the substrate.
M + OH {{eqm}} M(OH);{{spaces|5}}
In water the concentration of hydroxide is related to the concentration of hydrogen ions by the self-ionization constant, Kw.
Kw=[H+][OH−];{{spaces|5}}[OH−] = Kw[H+]−1
The expression for hydroxide concentration is substituted into the formation constant expression
The literature usually gives value of β*.
Acid–base complexes
{{Main|acid–base equilibrium}}A Lewis acid, A, and a Lewis base, B, can be considered to form a complex AB
A + B {{eqm}} AB{{spaces|5}}
There are three major theories relating to the strength of Lewis acids and bases and the interactions between them.
- Hard and soft acid–base theory (HSAB).&91;10&93; This is used mainly for qualitative purposes.
- Drago and Wayland proposed a two-parameter equation which predicts the standard enthalpy of formation of a very large number of adducts quite accurately. {{nowrap begin}}−ΔH⊖ (A − B) = EAEB + CACB.{{nowrap end}} Values of the E and C parameters are available&91;11&93;
- Guttmann donor numbers: for bases the number is derived from the enthalpy of reaction of the base with antimony pentachloride in 1,2-Dichloroethane as solvent. For acids, an acceptor number is derived from the enthalpy of reaction of the acid with triphenylphosphine oxide.&91;12&93;
For more details see: acid–base reaction, acid catalysis, acid–base extraction.
Thermodynamics
The thermodynamics of metal ion complex formation provides much significant information.[13] In particular it is useful in distinguishing between enthalpic and entropic effects. Enthalpic effects depend on bond strengths and entropic effects have to do with changes in the order/disorder of the solution as a whole. The chelate effect, below, is best explained in terms of thermodynamics.
An equilibrium constant is related to the standard Gibbs free energy change for the reaction
ΔG⊖ = −2.303 RT log10 β.
R is the gas constant and T is the absolute temperature. At 25 °C, {{nowrap|1=ΔG⊖ = (−5.708 kJ mol−1) ⋅ log β}}. Free energy is made up of an enthalpy term and an entropy term.
ΔG⊖ = ΔH⊖ − TΔS⊖
The standard enthalpy change can be determined by calorimetry or by using the Van 't Hoff equation, though the calorimetric method is preferable. When both the standard enthalpy change and stability constant have been determined, the standard entropy change is easily calculated from the equation above.
The fact that stepwise formation constants of complexes of the type MLn decrease in magnitude as n increases may be partly explained in terms of the entropy factor. Take the case of the formation of octahedral complexes.
[M(H2O)mLn−1] + L {{eqm}} [M(H2O)m−1Ln]
For the first step m = 6, n = 1 and the ligand can go into one of 6 sites. For the second step m = 5 and the second ligand can go into one of only 5 sites. This means that there is more randomness in the first step than the second one; ΔS⊖ is more positive, so ΔG⊖ is more negative and log K1 > log K2. The ratio of the stepwise stability constants can be calculated on this basis, but experimental ratios are not exactly the same because ΔH⊖ is not necessarily the same for each step.[14] The entropy factor is also important in the chelate effect, below.
Ionic strength dependence
The thermodynamic equilibrium constant, K⊖, for the equilibrium
M + L {{eqm}} ML
can be defined[15] as
where {ML} is the activity of the chemical species ML etc. K⊖ is dimensionless since activity is dimensionless. Activities of the products are placed in the numerator, activities of the reactants are placed in the denominator. See activity coefficient for a derivation of this expression.
Since activity is the product of concentration and activity coefficient (γ) the definition could also be written as
where [ML] represents the concentration of ML and Γ is a quotient of activity coefficients. This expression can be generalized as
To avoid the complications involved in using activities, stability constants are determined, where possible, in a medium consisting of a solution of a background electrolyte at high ionic strength, that is, under conditions in which Γ can be assumed to be always constant.[15] For example, the medium might be a solution of 0.1 mol dm−3 sodium nitrate or 3 mol dm−3 sodium perchlorate. When Γ is constant it may be ignored and the general expression in theory, above, is obtained.
All published stability constant values refer to the specific ionic medium used in their determination and different values are obtained with different conditions, as illustrated for the complex CuL (L = glycinate). Furthermore, stability constant values depend on the specific electrolyte used as the value of Γ is different for different electrolytes, even at the same ionic strength. There does not need to be any chemical interaction between the species in equilibrium and the background electrolyte, but such interactions might occur in particular cases. For example, phosphates form weak complexes with alkali metals, so, when determining stability constants involving phosphates, such as ATP, the background electrolyte used will be, for example, a tetralkylammonium salt. Another example involves iron(III) which forms weak complexes with halide and other anions, but not with perchlorate ions.
When published constants refer to an ionic strength other than the one required for a particular application, they may be adjusted by means of specific ion theory (SIT) and other theories.[17]
Temperature dependence
All equilibrium constants vary with temperature according to the Van 't Hoff equation[18]
Alternatively
R is the gas constant and T is the thermodynamic temperature. Thus, for exothermic reactions, where the standard enthalpy change, ΔH⊖, is negative, K decreases with temperature, but for endothermic reactions, where ΔH⊖ is positive, K increases with temperature.
Factors affecting the stability constants of complexes
The chelate effect
Consider the two equilibria, in aqueous solution, between the copper(II) ion, Cu2+ and ethylenediamine (en) on the one hand and methylamine, MeNH2 on the other.
{{NumBlk|:|Cu2+ + en {{eqm}} [Cu(en)]2+|{{EquationRef|1}}}}{{NumBlk|:|Cu2+ + 2 MeNH2 {{eqm}} [Cu(MeNH2)2]2+|{{EquationRef|2}}}}In {{EquationNote|(1)}} the bidentate ligand ethylene diamine forms a chelate complex with the copper ion. Chelation results in the formation of a five-membered ring. In {{EquationNote|(2)}} the bidentate ligand is replaced by two monodentate methylamine ligands of approximately the same donor power, meaning that the enthalpy of formation of Cu–N bonds is approximately the same in the two reactions. Under conditions of equal copper concentrations and when then concentration of methylamine is twice the concentration of ethylenediamine, the concentration of the complex {{EquationNote|(1)}} will be greater than the concentration of the complex {{EquationNote|(2)}}. The effect increases with the number of chelate rings so the concentration of the EDTA complex, which has six chelate rings, is much higher than a corresponding complex with two monodentate nitrogen donor ligands and four monodentate carboxylate ligands. Thus, the phenomenon of the chelate effect is a firmly established empirical fact: under comparable conditions, the concentration of a chelate complex will be higher than the concentration of an analogous complex with monodentate ligands.
The thermodynamic approach to explaining the chelate effect considers the equilibrium constant for the reaction: the larger the equilibrium constant, the higher the concentration of the complex.
{{NumBlk|:|[Cu(en)] {{=}} β11[Cu][en]|{{EquationRef|3}}}}{{NumBlk|:|[Cu(MeNH2)2] {{=}} β12[Cu][MeNH2]2|{{EquationRef|4}}}}When the analytical concentration of methylamine is twice that of ethylenediamine and the concentration of copper is the same in both reactions, the concentration [Cu(en)]2+ is much higher than the concentration [Cu(MeNH2)2]2+ because {{math|β11 ≫ β12.}}
| Deferiprone | Penicillamine | triethylenetetramine, TETA | Ethylenediaminetetraacetic acid, EDTA |
| Diethylenetriaminepentaacetic acid, DTPA | Valinomycin | Tri-n-butyl phosphate |
An ion-exchange resin such as chelex 100, which contains chelating ligands bound to a polymer, can be used in water softeners and in chromatographic separation techniques. In solvent extraction the formation of electrically-neutral complexes allows cations to be extracted into organic solvents. For example, in nuclear fuel reprocessing uranium(VI) and plutonium(VI) are extracted into kerosene as the complexes [MO2(TBP)2(NO3)2] (TBP = tri-n-butyl phosphate). In phase-transfer catalysis, a substance which is insoluble in an organic solvent can be made soluble by addition of a suitable ligand. For example, potassium permanganate oxidations can be achieved by adding a catalytic quantity of a crown ether and a small amount of organic solvent to the aqueous reaction mixture, so that the oxidation reaction occurs in the organic phase.
In all these examples, the ligand is chosen on the basis of the stability constants of the complexes formed. For example, TBP is used in nuclear fuel reprocessing because (among other reasons) it forms a complex strong enough for solvent extraction to take place, but weak enough that the complex can be destroyed by nitric acid to recover the uranyl cation as nitrato complexes, such as [UO2(NO3)4]2− back in the aqueous phase.
Supramolecular complexes
Supramolecular complexes are held together by hydrogen bonding, hydrophobic forces, van der Waals forces, π-π interactions, and electrostatic effects, all of which can be described as noncovalent bonding. Applications include molecular recognition, host–guest chemistry and anion sensors.
A typical application in molecular recognition involved the determination of formation constants for complexes formed between a tripodal substituted urea molecule and various saccharides.[32] The study was carried out using a non-aqueous solvent and NMR chemical shift measurements. The object was to examine the selectivity with respect to the saccharides.
An example of the use of supramolecular complexes in the development of chemosensors is provided by the use of transition-metal ensembles to sense for ATP.[33]
Anion complexation can be achieved by encapsulating the anion in a suitable cage. Selectivity can be engineered by designing the shape of the cage. For example, dicarboxylate anions could be encapsulated in the ellipsoidal cavity in a large macrocyclic structure containing two metal ions.[34]
Experimental methods
{{main|Determination of equilibrium constants}}The method developed by Bjerrum is still the main method in use today, though the precision of the measurements has greatly increased. Most commonly, a solution containing the metal ion and the ligand in a medium of high ionic strength is first acidified to the point where the ligand is fully protonated. This solution is then titrated, often by means of a computer-controlled auto-titrator, with a solution of CO2-free base. The concentration, or activity, of the hydrogen ion is monitored by means of a glass electrode. The data set used for the calculation has three components: a statement defining the nature of the chemical species that will be present, called the model of the system, details concerning the concentrations of the reagents used in the titration, and finally the experimental measurements in the form of titre and pH (or emf) pairs.
It is not always possible to use a glass electrode. If that is the case, the titration can be monitored by other types of measurement. Absorbance spectra, fluorescence spectra and NMR spectra are the most commonly used alternatives. Current practice is to take absorbance or fluorescence measurements at a range of wavelengths and to fit these data simultaneously. Various NMR chemical shifts can also be fitted together.
The chemical model will include values of the protonation constants of the ligand, which will have been determined in separate experiments, a value for log Kw and estimates of the unknown stability constants of the complexes formed. These estimates are necessary because the calculation uses a non-linear least-squares algorithm. The estimates are usually obtained by reference to a chemically similar system. The stability constant databases[8][9] can be very useful in finding published stability constant values for related complexes.
In some simple cases the calculations can be done in a spreadsheet.[35] Otherwise, the calculations are performed with the aid of a general-purpose computer programs. The most frequently used programs are:
- Potentiometric and/or spectrophotometric data: PSEQUAD[36]
- Potentiometric data: HYPERQUAD,[37] BEST[38]
- Spectrophotometric data: HypSpec, SQUAD,[39] SPECFIT,[40][41] ReactLab EQUILIBRIA.[42]
- NMR data HypNMR,[43] WINEQNMR2[44]
In biochemistry, formation constants of adducts may be obtained from Isothermal titration calorimetry (ITC) measurements. This technique yields both the stability constant and the standard enthalpy change for the equilibrium.[45] It is mostly limited, by availability of software, to complexes of 1:1 stoichiometry.
Critically evaluated data
The following references are for critical reviews of published stability constants for various classes of ligands. All these reviews are published by IUPAC and the full text is available, free of charge, in pdf format.
- ethylenediamine (en) [46]
- Nitrilotriacetic acid (NTA)[47]
- aminopolycarboxylic acids (complexones)[48]
- Alpha hydroxy acids and other hydroxycarboxylic acids[49][50]
- crown ethers[51]
- phosphonic acids[52][53]
- imidazoles and histamines[54]
- amino acids with polar side-chains[55]
- nucleotides[56]
- acetylacetone[57]
- general[58]
- Chemical speciation of environmentally significant heavy metals with inorganic ligands. Part 1: The Hg2+–Cl−, OH−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} systems.[59]
- Chemical speciation of environmentally significant metals with inorganic ligands Part 2: The Cu2+–OH−, Cl−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} aqueous systems[60]
- Chemical speciation of environmentally significant metals with inorganic ligands Part 3: The Pb2+–OH−, Cl−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} systems[61]
- Chemical speciation of environmentally significant metals with inorganic ligands. Part 4: The Cd2+–OH−, Cl−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} systems[62]
Databases
- The Ki Database is a public domain database of published binding affinities (Ki) of drugs and chemical compounds for receptors, neurotransmitter transporters, ion channels, and enzymes.
- BindingDB is a public domain database of measured binding affinities, focusing chiefly on the interactions of protein considered to be drug-targets with small, drug-like molecules
References
2. ^{{cite book |title=Chemistry of Complex Equilibria |last=Beck |first=M. T. |last2=Nagypál|first2= I. |year=1990 |publisher=Horwood |isbn=0-85312-143-5|chapter=Chapter 1}}
3. ^{{cite book |title=The Determination of Stability Constants |last=Rossotti |first=F. J. C. |last2=Rossotti|first2= H. |year=1961 |publisher=McGraw–Hill}}
4. ^{{cite journal|last=Dyrssen|first=D.|last2=Ingri|first2= N. |last3=Sillen|first3= L. G. |year=1961|title=Pit-mapping - A general approach to Computer refinement of stability constants.|journal=Acta Chem. Scand.|volume=15|pages=694–696|doi=10.3891/acta.chem.scand.15-0694}}
5. ^{{cite journal|last=Ingri|first=N.|last2=Sillen|first2= L. G. |year=1964|title=High-speed computers as a supplement to graphical methods, IV. An ALGOL version of LETAGROP-VRID|journal=Arkiv för Kemi|volume=23|pages=97–121}}
6. ^{{cite journal|last=Sayce|first=I. G.|year=1968|title=Computer calculations of equilibrium constantsof species present in mixtures of metal ions and complexing reagents|journal=Talanta|volume=15|pages=1397–1421|pmid=18960446|issue=12|doi=10.1016/0039-9140(68)80200-0}}
7. ^{{cite journal|last=Sabatini|first=A.|last2=Vacca |first2=A. |last3=Gans|first3= P. |year=1974|title=MINIQUAD - A general computer program for the computation of Stability constants|journal=Talanta|volume=21|pages=53–77|doi=10.1016/0039-9140(74)80063-9|pmid=18961420|issue=1}}
8. ^1 IUPAC SC-Database A comprehensive database of published data on equilibrium constants of metal complexes and ligands
9. ^1 NIST Standard Reference Database 46 Critically Selected Stability Constants of Metal Complexes
10. ^{{cite book|last=Pearson|first=R. G.|title=Chemical Hardness: Applications from Molecules to Solids |publisher=Springer-VCH|year=1997|isbn=3-527-29482-1 }}
11. ^{{cite journal|last=Drago| first=R. S. |last2=Wong |first2=N. |last3=Bilgrien |first3=C. |last4= Vogel|first4= C. |title=E and C parameters from Hammett substituent constants and use of E and C to understand cobalt–carbon bond energies|year=1987|journal=Inorg. Chem.|volume=26|issue=1|pages=9–14|doi=10.1021/ic00248a003}}
12. ^{{cite book|last=Gutmann|first=V.|title=The Donor–Acceptor Approach to Molecular Interactions|publisher=Springer|year=1978|isbn=0-306-31064-3 }}
13. ^{{cite book|first=F. J. C. |last=Rossotti|title=Modern coordination chemistry|editor1-last=Lewis|editor1-first= J.|editor2-first= Wilkins|editor2-last= R. G.|publisher=Interscience|location=New York|year=1960|chapter=The thermodynamics of metal ion complex formation in solution}}
14. ^{{cite book |title=Chemistry of Complex Equilibria |last=Beck |first=M. T. |last2=Nagypál|first2= I. |year=1990 |publisher=Horwood |isbn=0-85312-143-5}} sections 3.5.1.2, 6.6.1 and 6.6.2
15. ^1 {{cite book |title=The Determination of Stability Constants |last=Rossotti |first=F. J. C. |last2=Rossotti|first2= H. |year=1961 |publisher=McGraw–Hill|chapter= Chapter 2: Activity and Concentration Quotients}}
16. ^{{cite journal|last=Gergely|first=A.|last2=Nagypál|first2=I. |first3=Farkas|last3= E. |year=1974|title=A réz(II)-aminosav törzskomplexek vizes oldatában lejátszodó protoncsere-reakciók kinetikájának NMR-vizsgálata |trans-title=NMR study of the proton exchange process in aqueous solutions of copper(II)-aminoacid parent complexes|journal=Magyar Kémiai Folyóirat|volume=80|pages=545–549 }}
17. ^{{cite web |url = http://www.iupac.org/web/ins/2000-003-1-500 |title = Project: Ionic Strength Corrections for Stability Constants |publisher = IUPAC |accessdate = 2008-11-23 |deadurl = yes |archiveurl = https://web.archive.org/web/20081029193538/http://www.iupac.org/web/ins/2000-003-1-500 |archivedate = 2008-10-29 |df = }}
18. ^{{cite book |title=Physical Chemistry |last=Atkins |first=P. W. |last2=De Paula|first2= J. |year=2006 |publisher=Oxford University Press |isbn=0-19-870072-5|chapter= Section 7.4: The Response of Equilibria to Temperature}}
19. ^1 {{Greenwood&Earnshaw}} p. 910
20. ^{{cite journal |last=Schwarzenbach |first=G. |year=1952 |title=Der Chelateffekt |trans-title=The Chelate Effect|journal=Helv. Chim. Acta|volume=35 |issue=7|pages=2344–2359|doi=10.1002/hlca.19520350721}}
21. ^{{cite journal|last=Cabinness|first=D. K.|last2=Margerum|first2= D. W. |year=1969|title=Macrocyclic effect on the stability of copper(II) tetramine complexes|journal=J. Am. Chem. Soc.|volume=91|issue=23|pages=6540–6541|doi=10.1021/ja01051a091}}
22. ^{{cite book|last=Lindoy|first=L. F.|authorlink=Leonard Francis Lindoy|title=The Chemistry of Macrocyclic Ligand Complexes|publisher=Cambridge University Press|year=1990|isbn=0-521-40985-3|chapter= Chapter 6: Thermodynamic considerations}}
23. ^{{cite journal|last=Pedersen|first=C. J. |year=1967|journal=J. Am. Chem. Soc.|volume=89|title=Cyclic polyethers and their complexes with metal salts|issue=26|pages= 7017–7036|doi=10.1021/ja01002a035}}
24. ^{{Greenwood&Earnshaw}} p. 1100, Figure 25.7
25. ^{{cite journal|last=Lundeen|first=M.|last2=Hugus|first2=Z. Z.|year=1992|title=A calorimetric study of some metal ion complexing equilibria |journal=Thermochim. Acta|volume=196|issue=1|pages=93–103 |doi=10.1016/0040-6031(92)85009-K}}
26. ^{{cite journal|last=Ahrland|first=S.|last2=Chatt|first2 =J. |last3=Davies|first3= N. R. |year=1958|title=The relative affinities of ligand atoms for acceptor molecules and ions|journal=Quart. Rev.|volume=12|issue=3|pages=265–276|doi=10.1039/QR9581200265}}
27. ^{{cite journal|title=Hard and Soft Acids and Bases|last=Pearson|first= R. G.|journal= J. Am. Chem. Soc. |year=1963| volume= 85 |issue=22|pages=3533–3539|doi=10.1021/ja00905a001}}
28. ^{{cite book |title=Chemistry of Complex Equilibria |last=Beck |first=M. T. |last2=Nagypál|first2= I. |year=1990 |publisher=Horwood |isbn=0-85312-143-5 |page=354}}
29. ^{{cite journal |last=Irving | first = H. M. N. H. |last2=Williams|first2= R. J. P. |year=1953|title=The stability of transition-metal complexes|journal=J. Chem. Soc.|pages=3192–3210|doi=10.1039/JR9530003192 }}
30. ^{{cite journal|last=Arena|first=G.|last2=Contino|first2=A.|last3=Longo |first3=E.|last4=Sciotto|first4=D. |last5=Spoto|first5=G. |year=2001|title=Selective complexation of soft Pb2+ and Hg2+ by a novel allyl functionalized thioamide calix[4]arene in 1,3-alternate conformation: a UV-visible and H-1 NMR spectroscopic investigation|journal=J. Chem. Soc., Perkin Trans.|volume= 2|issue=12|pages=2287–2291|doi=10.1039/b107025h}}
31. ^{{cite book|last=Runge|first=V. M.|last2=Scott|first2=S. |title=Contrast-enhanced Clinical Magnetic Resonance Imaging |publisher=University Press of Kentucky|year=1998|isbn=0-8131-1944-8}}
32. ^{{cite journal|last=Vacca|first=A.|last2=Nativi|first2= C. |last3=Cacciarini|first3= M. |last4=Pergoli|first4= R. |last5= Roelens|first5= S. |year=2004|title=A New Tripodal Receptor for Molecular Recognition of Monosaccharides. A Paradigm for Assessing Glycoside Binding Affinities and Selectivities by 1H NMR Spectroscopy|journal=J. Am. Chem. Soc.|volume=126|pages=16456–16465|doi= 10.1021/ja045813s|pmid=15600348|issue=50}}
33. ^{{cite journal|last=Marcotte|first=N.|last2=Taglietti |first2=A. |year=2003|title=Transition-metal-based chemosensing ensembles: ATP sensing in physiological conditions|journal= Supramol. Chem.|volume=15|issue=7|pages=617–717|doi=10.1080/10610270310001605205 }}
34. ^{{cite journal|last=Boiocchi|first=M.|last2=Bonizzoni|first2= M.|last3=Fabbrizzi|first3= L. |last4=Piovani|first4= G. |last5= Taglietti|first5= A. |year=2004|title=A dimetallic cage with a long ellipsoidal cavity for the fluorescent detection of dicarboxylate anions in water|journal=Angew. Chem. Int. Ed.|volume=43|pages=3847–3852|doi=10.1002/anie.200460036|pmid=15258953|issue=29 }}
35. ^{{cite book|last=Billo|first=E. J.|title=Excel for Chemists: A comprehensive guide|publisher=Wiley-VCH|year=1997|edition=2nd|chapter=Chapter 22|isbn=0-471-18896-4}}
36. ^{{cite book|last=Zekany|first=L.|last2=Nagypál|first2= I. |title=Computational methods for the determination of formation constants|editor=Leggett|publisher=Plenum|year=1985|chapter=Chapter 8: PSEQUAD: A comprehensive program for the evaluation of potentiometric and/or spectrophotometric equilibrium data using analytical derivatives|isbn=0-306-41957-2}}
37. ^{{cite journal|last=Gans|first=P.|last2=Sabatini|first2= A. |last3=Vacca|first3= A. |year=1996|title=Investigation of equilibria in solution. Determination of equilibrium constants with the HYPERQUAD suite of programs|journal=Talanta|volume=43|pages=1739–1753|doi=10.1016/0039-9140(96)01958-3|pmid=18966661|issue=10}}
38. ^{{cite book|first1=A. E.|last1= Martell |first2= R. J. |last2=Motekaitis|title=The determination and use of stability constants|publisher=Wiley-VCH|date=1992}}
39. ^{{cite book|last=Leggett|first=D.|title=Computational methods for the determination of formation constants|editor=Leggett|publisher=Plenum|year=1985|chapter=Chapter 6: SQUAD: Stability quotients from absorbance data|isbn=0-306-41957-2}}
40. ^{{cite journal|last=Gampp|first=M.|last2=Maeder|first2= M. |last3=Mayer|first3= C. J. |last4= Zuberbühler|first4= A. D.|title=Calculation of equilibrium constants from multiwavelength spectroscopic data—I : Mathematical considerations |journal=Talanta|volume=32|pages=95–101|doi=10.1016/0039-9140(85)80035-7|year=1985|pmid=18963802|issue=2}}
41. ^{{cite journal|last=Gampp|first=M.|last2=Maeder|first2= M. |last3=Mayer|first3= C. J. |last4= Zuberbühler|first4= A. D.|title=Calculation of equilibrium constants from multiwavelength spectroscopic data—II1: Specfit: two user-friendly programs in basic and standard fortran 77|journal=Talanta|publisher=1995|volume=32|pages=251–264 |doi=10.1016/0039-9140(85)80077-1|year=1985|pmid=18963840|issue=4}}
42. ^Jplus Consulting Pty Ltd
43. ^{{cite journal|last=Frassineti|first=C.|last2=Alderighi|first2=L. |last3=Gans|first3= P. |last4=Sabatini|first4=A. |last5=Vacca|first5=A. |last6= Ghelli|first6= S. |year=2003|title=Determination of protonation constants of some fluorinated polyamines by means of 13C NMR data processed by the new computer program HypNMR2000. Protonation sequence in polyamines|journal=Anal. Bioanal. Chem.|volume=376|pages=1041–1052|doi=10.1007/s00216-003-2020-0|pmid=12845401|issue=7}}
44. ^{{cite journal|last=Hynes|first=M. J.|year=1993|title=EQNMR: A computer program for the calculation of stability constants from nuclear magnetic resonance chemical shift data|journal=J. Chem. Soc., Dalton Trans.|issue=2|pages=311–312|doi=10.1039/DT9930000311}}
45. ^{{cite book |last=O'Brien |first=R. |last2=Ladbury|first2= J. E. |last3=Chowdry|first3= B. Z. |title=Protein-Ligand interactions: hydrodynamics and calorimetry |editor1-last=Harding|editor1-first= S. E.|editor2-last= Chowdry|editor2-first= B. Z. |publisher=Oxford University Press |year=2000 |chapter=Chapter 10 |isbn=0-19-963749-0 }}
46. ^{{cite journal|last=Paoletti|first=P.|year=1984|title=Formation of metal complexes with ethylenediamine: a critical survey of equilibrium constants, enthalpy and entropy values|journal=Pure Appl. Chem.|volume= 56|issue=4|pages=491–522|doi=10.1351/pac198456040491| url=http://www.iupac.org/publications/pac/pdf/1984/pdf/5604x0491.pdf}}
47. ^{{cite journal|last=Anderegg|first=G.|year=1982|title=Critical survey of stability constants of NTA complexes|journal=Pure Appl. Chem.|volume=54|issue=12|pages=2693–2758|doi=10.1351/pac198254122693|url=http://iupac.org/publications/pac/pdf/1982/pdf/5412x2693.pdf}}
48. ^{{cite journal|last=Anderegg|first=G |last2=Arnaud-Neu|first2=F. |last3=Delgado|first3=R. |last4=Felcman|first4=J. |last5=Popov|first5= K.|year=2003|title=Critical evaluation of stability constants of metal complexes of complexones for biomedical and environmental applications (IUPAC Technical Report)|journal=Pure Appl. Chem.|volume=77|issue=8|pages=1445–95|doi=10.1351/pac200577081445|url=http://iupac.org/publications/pac/pdf/2005/pdf/7708x1445.pdf}}
49. ^{{cite journal|last=Lajunen|first=L. H. J.|last2=Portanova|first2=R. |last3=Piispanen|first3= J. |last4= Tolazzi|first4= M. |year=1997|title=Critical evaluation of stability constants for alpha-hydroxycarboxylic acid complexes with protons and metal ions and the accompanying enthalpy changes. Part I: Aromatic ortho-hydroxycarboxylic acids (Technical Report)|journal=Pure Appl. Chem.|volume=69|issue=2|pages=329–382|doi=10.1351/pac199769020329|url=http://iupac.org/publications/pac/pdf/1997/pdf/6902x0329.pdf}}
50. ^{{cite journal |last=Portanova |first=R |last2=Lajunen|first2= L. H. J. |last3=Tolazzi|first3= M. |last4= Piispanen|first4= J. |year=2003|title=Critical evaluation of stability constants for alpha-hydroxycarboxylic acid complexes with protons and metal ions and the accompanying enthalpy changes. Part II. Aliphatic 2-hydroxycarboxylic acids (IUPAC Technical Report)|journal=Pure Appl. Chem.|volume=75|issue=4|pages=495–540|doi=10.1351/pac200375040495|url=http://iupac.org/publications/pac/pdf/2003/pdf/7504x0495.pdf}}
51. ^{{cite journal|last=Arnaud-Neu|first=F.|last2=Delgado|first2= R. |last3=Chaves|first3= S. |year=2003|title=Critical evaluation of stability constants and thermodynamic functions of metal complexes of crown ethers (IUPAC Technical Report)|journal=Pure Appl. Chem.|volume=75|issue=1|pages=71–102|doi=10.1351/pac200375010071|url=http://iupac.org/publications/pac/pdf/2003/pdf/7501x0071.pdf}}
52. ^{{cite journal|last=Popov|first=K.|last2=Rönkkömäki|first2= H. |last3=Lajunen|first3= L. H. J. |year=2001|title=Critical evaluation of stability constants of phosphonic acids (IUPAC Technical Report)|journal=Pure Appl. Chem.|volume=73|issue=11|pages=1641–1677|doi=10.1351/pac200173101641|url=http://iupac.org/publications/pac/pdf/2001/pdf/7310x1641.pdf}}
53. ^{{cite journal|last=Popov|first=K.|last2=Rönkkömäki|first2= H. |last3=Lajunen|first3= L. H. J. |year=2002|title=Errata|journal=Pure Appl. Chem.|volume=74|issue=11|pages=2227–2227|doi=10.1351/pac200274112227|url=http://iupac.org/publications/pac/pdf/2002/pdf/7411x2227.pdf}}
54. ^{{cite journal|last=Sjöberg|first=S.|year=1997|title=Critical evaluation of stability constants of metal-imidazole and metal-histamine systems (Technical Report)|journal=Pure Appl. Chem.|volume=69|issue=7|pages=1549–1570|doi=10.1351/pac199769071549|url=http://iupac.org/publications/pac/pdf/1997/pdf/6907x1549.pdf}}
55. ^{{cite journal|last=Berthon|first=G.|year=1995|title=Critical evaluation of the stability constants of metal complexes of amino acids with polar side chains (Technical Report)|journal=Pure Appl. Chem.|volume=67|issue=7|pages=1117–1240|doi=10.1351/pac199567071117|url=http://iupac.org/publications/pac/pdf/1995/pdf/6707x1117.pdf}}
56. ^{{cite journal|last=Smith|first=R. M.|last2=Martell |first2=A. E. |last3=Chen|first3= Y. |year=1991|title=Critical evaluation of stability constants for nucleotide complexes with protons and metal ions and the accompanying enthalpy changes|journal=Pure Appl. Chem.|volume=63|issue=7|pages=1015–1080|doi=10.1351/pac199163071015|url=http://iupac.org/publications/pac/pdf/1991/pdf/6307x1015.pdf}}
57. ^{{cite journal|last=Stary|first=J.|last2=Liljenzin|first2= J. O. |year=1982|title=Critical evaluation of equilibrium constants involving acetylacetone and its metal chelates|journal=Pure Appl. Chem.|volume=54|issue=12|pages=2557–2592|doi=10.1351/pac198254122557|url=http://iupac.org/publications/pac/pdf/1982/pdf/5412x2557.pdf}}
58. ^{{cite journal|last=Beck|first=M. T.|year=1977|title=Critical evaluation of equilibrium constants in solution. Stability constants of metal complexes|journal=Pure Appl. Chem.|volume=49|issue=1|pages=127–136|doi=10.1351/pac197749010127|url=http://iupac.org/publications/pac/pdf/1977/pdf/4901x0127.pdf}}
59. ^{{cite journal|last=Powell|first=Kipton, J.|last2=Brown|first2=Paul L. |last3=Byrne|first3=Robert H. |last4=Gajda|first4=Tamás |last5=Hefter|first5=Glenn |last6=Sjöberg|first6= Staffan |last7= Wanner|first7= Hans |year=2005|title=Chemical speciation of environmentally significant heavy metals with inorganic ligands. Part 1: The Hg2+–Cl−, OH−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} aqueous systems|journal=Pure Appl. Chem.|volume=77|issue=4|pages=739–800|doi=10.1351/pac200577040739|url=http://www.iupac.org/publications/pac/pdf/2005/pdf/7704x0739.pdf}}
60. ^{{cite journal|last=Powell|first=Kipton J.|last2=Brown|first2=Paul L. |last3=Byrne|first3=Robert H. |last4=Gajda|first4=Tamás |last5=Hefter|first5=Glenn |last6=Sjöberg|first6= Staffan |last7= Wanner|first7= Hans |year=2007|title=Chemical speciation of environmentally significant metals with inorganic ligands Part 2: The Cu2+–OH−, Cl−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} systems|journal=Pure Appl. Chem.|volume=79|issue=5|pages=895–950|doi=10.1351/pac200779050895|url=http://www.iupac.org/publications/pac/pdf/2007/pdf/7905x0895.pdf}}
61. ^{{cite journal|last=Powell|first=Kipton J.|last2=Brown|first2=Paul L. |last3=Byrne|first3=Robert H. |last4=Gajda|first4=Tamás |last5=Hefter|first5=Glenn |last6=Leuz|first6= Ann-Kathrin |last7=Sjöberg|first7= Staffan |last8= Wanner|first8= Hans |year=2009|title=Chemical speciation of environmentally significant metals with inorganic ligands Part 3: The Pb2+–OH−, Cl−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} systems|journal=Pure Appl. Chem.|volume=81|issue=12|pages=2425–2476 |doi=10.1351/PAC-REP-09-03-05|url=http://www.iupac.org/publications/pac/pdf/2009/pdf/8112x2425.pdf}}
62. ^{{cite journal|last=Powell|first=Kipton J.|last2=Brown|first2=Paul L. |last3=Byrne|first3=Robert H. |last4=Gajda|first4=Tamás |last5=Hefter|first5=Glenn |last6=Leuz|first6= Ann-Kathrin |last7=Sjöberg|first7= Staffan |last8= Wanner|first8= Hans |year=2011|title=Chemical speciation of environmentally significant metals with inorganic ligands. Part 4: The Cd2+–OH−, Cl−, {{chem|CO|3|2−}}, {{chem|SO|4|2−}}, and {{chem|PO|4|3−}} systems|journal=Pure Appl. Chem.|volume=83|issue=5|pages=1163–1214|doi=10.1351/PAC-REP-10-08-09|url=http://www.iupac.org/publications/pac/pdf/2011/pdf/8305x1163.pdf}}
Further reading
{{cite book|last1=Sigel
|first1=Roland K. O.
|last2=Skilandat
|first2=Miriam
|last3=Sigel
|first3=Astrid
|last4=Operschall
|first4=Bert P.
|last5=Sigel
|first5=Helmut
|editor1-first=Astrid |editor1-last=Sigel|editor2-first= Helmut |editor2-last=Sigel |editor3-first=Roland K. O. |editor3-last=Sigel
|title=Cadmium: From Toxicology to Essentiality
|series=Metal Ions in Life Sciences
|volume=11
|year=2013
|publisher=Springer
|pages=191–274
|chapter=Chapter 8. Complex formation of cadmium with sugar residues, nucleobases, phosphates, nucleotides and nucleic acids
|doi=10.1007/978-94-007-5179-8_8}}{{cite book
|last1=Sóvágó
|first1=Imre
|last2=Várnagy
|first2=Katalin
|editor1-first=Astrid |editor1-last=Sigel|editor2-first= Helmut |editor2-last=Sigel |editor3-first=Roland K. O. |editor3-last=Sigel
|title=Cadmium: From Toxicology to Essentiality
|series=Metal Ions in Life Sciences
|volume=11
|year=2013
|publisher=Springer
|pages=275–302
|chapter=Chapter 9. Cadmium(II) complexes of amino acids and peptides
|doi=10.1007/978-94-007-5179-8_9}}{{cite book |last=Yatsimirsky |first=Konstantin Borisovich |title=Instability Constants of Complex Compounds |year=1960 |publisher=OUP |last2=Vasilyev|first2= Vladimir Pavlovich|translator-first= D. A.|translator-last= Patterson}}
External links
- Stability constants website: Contains information on computer programs, applications, databases and hardware for experimental titrations.
- Blues Train
- Blue streak
- Blue Streak (album)
- Bluestreak (Autobot)
- Bluestreak Cardinalfish
- Blue Streak missile
- Bluestreak (Transformerst)
- Blue-stripe blenny
- Blue-striped
- Bluestripe Darter
- Bluestriped blenny
- Bluestriped fangblenny
- Blue-striped Grunt
- Blue striped grunt
- Blue striped grunts
- Blue-striped Lizardfish
- Blue Striped Mime
- Bluestriped sabretooth blenny
- Blue striped snapper
- Bluestripe jack
- Bluestripe Snapper
- Blues turnaround
- Blue Sudoku
- Blue suit
- Blue suits