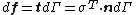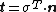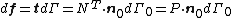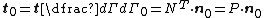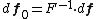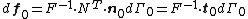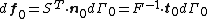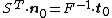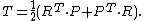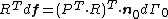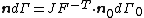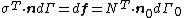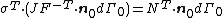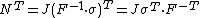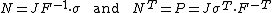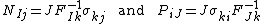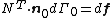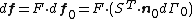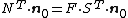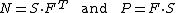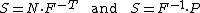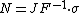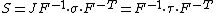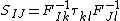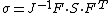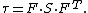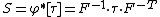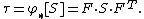- Definitions of stress measures Cauchy stress Kirchhoff stress Nominal stress/First Piola-Kirchhoff stress Second Piola-Kirchhoff stress Biot stress
- Relations between stress measures Relations between Cauchy stress and nominal stress Relations between nominal stress and second P-K stress Relations between Cauchy stress and second P-K stress
- See also
- Summary of relations between stress measures
- References
The most commonly used measure of stress is the Cauchy stress tensor, often called simply the stress tensor or "true stress". However, several other measures of stress can be defined.[1][2][3] Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:
- The Kirchhoff stress (
 ).
). - The Nominal stress (
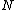 ).
). - The first Piola-Kirchhoff stress (
 ). This stress tensor is the transpose of the nominal stress (
). This stress tensor is the transpose of the nominal stress ( ).
). - The second Piola-Kirchhoff stress or PK2 stress (
 ).
). - The Biot stress (
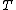 )
)
Definitions of stress measures
Consider the situation shown in the following figure. The following definitions use the notations shown in the figure.
In the reference configuration 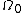 , the outward normal to a surface element
, the outward normal to a surface element 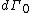 is
is 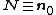 and the traction acting on that surface is
and the traction acting on that surface is 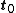 leading to a force vector
leading to a force vector 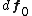 . In the deformed configuration
. In the deformed configuration  , the surface element changes to
, the surface element changes to 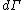 with outward normal
with outward normal  and traction vector
and traction vector 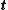 leading to a force
leading to a force 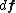 . Note that this surface can either be a hypothetical cut inside the body or an actual surface. The quantity
. Note that this surface can either be a hypothetical cut inside the body or an actual surface. The quantity 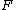 is the deformation gradient tensor,
is the deformation gradient tensor,  is its determinant.
is its determinant.
Cauchy stress
The Cauchy stress (or true stress) is a measure of the force acting on an element of area in the deformed configuration. This tensor is symmetric and is defined via
or
where 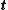 is the traction and
is the traction and  is the normal to the surface on which the traction acts.
is the normal to the surface on which the traction acts.
Kirchhoff stress
The quantity 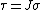 is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there
is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there
is no change in volume during plastic deformation). Another name for it is weighted Cauchy stress tensor.
Nominal stress/First Piola-Kirchhoff stress
The nominal stress 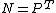 is the transpose of the first Piola-Kirchhoff stress (PK1 stress, also called engineering stress)
is the transpose of the first Piola-Kirchhoff stress (PK1 stress, also called engineering stress)  and is defined via
and is defined via
or
This stress is unsymmetric and is a two-point tensor like the deformation gradient.
The asymmetry derives from the fact that, as a tensor, it has one index attached to the reference configuration and one to the deformed configuration.[4]
Second Piola-Kirchhoff stress
If we pull back 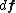 to the reference configuration, we have
to the reference configuration, we have
or,
The PK2 stress ( ) is symmetric and is defined via the relation
) is symmetric and is defined via the relation
Therefore,
Biot stress
The Biot stress is useful because it is energy conjugate to the right stretch tensor 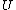 . The Biot stress is defined as the symmetric part of the tensor
. The Biot stress is defined as the symmetric part of the tensor 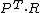 where
where 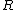 is the rotation tensor obtained from a polar decomposition of the deformation gradient. Therefore, the Biot stress tensor is defined as
is the rotation tensor obtained from a polar decomposition of the deformation gradient. Therefore, the Biot stress tensor is defined as
The Biot stress is also called the Jaumann stress.
The quantity 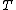 does not have any physical interpretation. However, the unsymmetrized Biot stress has the interpretation
does not have any physical interpretation. However, the unsymmetrized Biot stress has the interpretation
Relations between stress measures
Relations between Cauchy stress and nominal stress
From Nanson's formula relating areas in the reference and deformed configurations:
Now,
Hence,
or,
or,
In index notation,
Therefore,
Note that 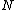 and
and  are not symmetric because
are not symmetric because 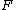 is not symmetric.
is not symmetric.
Relations between nominal stress and second P-K stress
Recall that
and
Therefore,
or (using the symmetry of  ),
),
In index notation,
Alternatively, we can write
Relations between Cauchy stress and second P-K stress
Recall that
In terms of the 2nd PK stress, we have
Therefore,
In index notation,
Since the Cauchy stress (and hence the Kirchhoff stress) is symmetric, the 2nd PK stress is also symmetric.
Alternatively, we can write
or,
Clearly, from definition of the push-forward and pull-back operations, we have
and
Therefore,  is the pull back of
is the pull back of  by
by 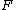 and
and  is the push forward of
is the push forward of  .
.
See also
- Stress (physics)
- Finite strain theory
- Continuum mechanics
- Hyperelastic material
- Cauchy elastic material
- Critical plane analysis
Summary of relations between stress measures
{{Navbox|name = Stress Tensor
|title = Stress Tensor
|listclass = hlist
|list1 =
- Cauchy stress tensor (
 )
) - First Piola-Kirchhoff stress tensor (
 )
) - Second Piola-Kirchhoff stress tensor (
 )
) - Kirchhoff stress tensor (
 )
) - Biot stress tensor (
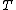 )
) - Mandel stress tensor (
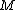 )
)
|state = show
}}
| Conversion formulae | ||||||
|---|---|---|---|---|---|---|
 |  |  |  | 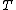 | 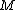 | |
 |  | 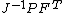 | 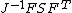 | 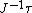 | 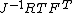 | 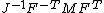 |
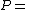 | 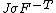 |  | 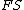 | 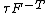 | 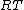 | 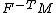 |
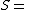 | 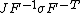 | 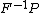 |  | 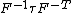 | 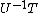 | 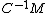 |
 | 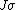 | 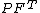 | 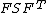 |  | 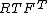 | 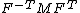 |
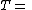 | 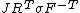 | 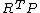 | 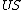 | 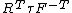 | 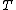 | 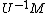 |
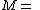 | 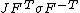 |  | 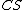 | 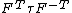 | 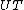 | 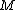 |
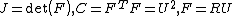 | ||||||
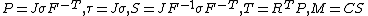 | ||||||
References
2. ^R. W. Ogden, 1984, Non-linear Elastic Deformations, Dover.
3. ^L. D. Landau, E. M. Lifshitz, Theory of Elasticity, third edition
4. ^{{cite book|title=Three-Dimensional Elasticity|url=https://books.google.com/books?id=tlGCC3w27iIC|date=1 April 1988|publisher=Elsevier|isbn=978-0-08-087541-5}}
- Liberaal Vlaams Verbond
- Libera Carlier
- Liberacci
- Liberace Museum Collection
- Liberachi
- Liberaci
- Liber ad honorem Augusti
- Libera (goddess)
- Liber AL
- Liberal Adventist
- Liberal Adventists
- Liberal Alliance
- Liberal Alliance (Chile)
- Liberal Alliance (Denmark)
- Liberal Alliance (Greece)
- Liberal Alternative
- Liberal anti-fascism
- Liberal anti-fascist
- Liberal Appeal
- Liberal Arts and Science Academy
- Liberal Arts and Science Academy of Austin at LBJ High School
- Liberal Arts Christian College, Lithuania
- Liberal arts colleges in the United States
- Liberal Arts, Inc.
- Liberal Arts, The Seven