请输入您要查询的百科知识：

　

词条 Succinct game
释义

  1. Types of succinct games

     Graphical games  Sparse games  Symmetric games  Anonymous games  Polymatrix games  Circuit games  Other representations 

  2. Summary of complexities of finding equilibria

  3. Notes

  4. External links

Consider a game of three players, I,II and III, facing, respectively, the strategies {T,B}, {L,R}, and {l,r}. Without further constraints, 3*23=24 utility values would be required to describe such a game.
L, lL, rR, lR, r
T{{fontcolor|red|4}}, {{fontcolor|green|6}}, {{fontcolor|blue|2}}{{fontcolor|red|5}}, {{fontcolor|green|5}}, {{fontcolor|blue|5}}{{fontcolor|red|8}}, {{fontcolor|green|1}}, {{fontcolor|blue|7}}{{fontcolor|red|1}}, {{fontcolor|green|4}}, {{fontcolor|blue|9}}
B{{fontcolor|red|8}}, {{fontcolor|green|6}}, {{fontcolor|blue|6}}{{fontcolor|red|7}}, {{fontcolor|green|4}}, {{fontcolor|blue|7}}{{fontcolor|red|9}}, {{fontcolor|green|6}}, {{fontcolor|blue|5}}{{fontcolor|red|0}}, {{fontcolor|green|3}}, {{fontcolor|blue|0}}
For each strategy profile, the utility of the first player is listed first ({{fontcolor|red|red}}), and is followed by the utilities of the second player ({{fontcolor|green|green}}) and the third player ({{fontcolor|blue|blue}}).

In algorithmic game theory, a succinct game or a succinctly representable game is a game which may be represented in a size much smaller than its normal form representation. Without placing constraints on player utilities, describing a game of players, each facing strategies, requires listing 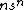utility values. Even trivial algorithms are capable of finding a Nash equilibrium in a time polynomial in the length of such a large input. A succinct game is of polynomial type if in a game represented by a string of length n the number of players, as well as the number of strategies of each player, is bounded by a polynomial in n (a formal definition, describing succinct games as a computational problem, is given by Papadimitriou & Roughgarden 2008[2]).

{{Clear}}

Types of succinct games

Graphical games

Say that each player's utility depends only on his own action and the action of one other player - for instance, I depends on II, II on III and III on I. Representing such a game would require only three 2x2 utility tables, containing in all only 12 utility values.
            !align="center"|''L''            !align="center"|''R''
{{fontcolor|red|9}}{{fontcolor|red|8}}
{{fontcolor|red|3}}{{fontcolor|red|4}}

|
            !align="center"|''l''            !align="center"|''r''

|-
|align="center"|{{fontcolor|green|6}}
|align="center"|{{fontcolor|green|8}}
|-
|align="center"|{{fontcolor|green|1}}
|align="center"|{{fontcolor|green|3}}
|}
|
            !align="center"|''T''            !align="center"|''B''

|-
|align="center"|{{fontcolor|blue|4}}
|align="center"|{{fontcolor|blue|4}}
|-
|align="center"|{{fontcolor|blue|5}}
|align="center"|{{fontcolor|blue|7}}
|}
|}

Graphical games are games in which the utilities of each player depends on the actions of very few other players. If is the greatest number of players by whose actions any single player is affected (that is, it is the indegree of the game graph), the number of utility values needed to describe the game is 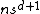, which, for a small is a considerable improvement.

It has been shown that any normal form game is reducible to a graphical game with all degrees bounded by three and with two strategies for each player.[3] Unlike normal form games, the problem of finding a pure Nash equilibrium in graphical games (if one exists) is NP-complete.[4] The problem of finding a (possibly mixed) Nash equilibrium in a graphical game is PPAD-complete.[5] Finding a correlated equilibrium of a graphical game can be done in polynomial time, and for a graph with a bounded treewidth, this is also true for finding an optimal correlated equilibrium.[2]

{{Clear}}

Sparse games

When most of the utilities are 0, as below, it is easy to come up with a succinct representation.
L, lL, rR, lR, r
T{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|0}}{{fontcolor|red|2}}, {{fontcolor|green|0}}, {{fontcolor|blue|1}}{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|0}}{{fontcolor|red|0}}, {{fontcolor|green|7}}, {{fontcolor|blue|0}}
B{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|0}}{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|0}}{{fontcolor|red|2}}, {{fontcolor|green|0}}, {{fontcolor|blue|3}}{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|0}}

Sparse games are those where most of the utilities are zero. Graphical games may be seen as a special case of sparse games.

For a two player game, a sparse game may be defined as a game in which each row and column of the two payoff (utility) matrices has at most a constant number of non-zero entries. It has been shown that finding a Nash equilibrium in such a sparse game is PPAD-hard, and that there does not exist a fully polynomial-time approximation scheme unless PPAD is in P.[7]

{{Clear}}

Symmetric games

purple|purple}}), and face the strategy set {T,B}. Let #TP and #BP be the number of a player's peers who've chosen T and B, respectively. Describing this game requires only 6 utility values.
            !align="center"|#TP=2
#BP=0            !align="center"|#TP=1
#BP=1            !align="center"|#TP=0
#BP=2
{{fontcolor|purple|5}}{{fontcolor|purple|2}}{{fontcolor|purple|2}}
{{fontcolor|purple|1}}{{fontcolor|purple|7}}{{fontcolor|purple|2}}

|}

In symmetric games all players are identical, so in evaluating the utility of a combination of strategies, all that matters is how many of the players play each of the strategies. Thus, describing such a game requires giving only 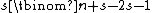utility values.

In a symmetric game with 2 strategies there always exists a pure Nash equilibrium – although a symmetric pure Nash equilibrium may not exist.[8] The problem of finding a pure Nash equilibrium in a symmetric game (with possibly more than two players) with a constant number of actions is in AC0; however, when the number of actions grows with the number of players (even linearly) the problem is NP-complete.[9] In any symmetric game there exists a symmetric equilibrium. Given a symmetric game of n players facing k strategies, a symmetric equilibrium may be found in polynomial time if k=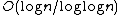.[10] Finding a correlated equilibrium in symmetric games may be done in polynomial time.[2]

{{Clear}}

Anonymous games

If players were different but did not distinguish between other players we would need to list 18 utility values to represent the game - one table such as that given for "symmetric games" above for each player.
            !align="center"|#TP=2
#BP=0            !align="center"|#TP=1
#BP=1            !align="center"|#TP=0
#BP=2
{{fontcolor|red|8}}, {{fontcolor|green|8}}, {{fontcolor|blue|2}}{{fontcolor|red|2}}, {{fontcolor|green|9}}, {{fontcolor|blue|5}}{{fontcolor|red|4}}, {{fontcolor|green|1}}, {{fontcolor|blue|4}}
{{fontcolor|red|6}}, {{fontcolor|green|1}}, {{fontcolor|blue|3}}{{fontcolor|red|2}}, {{fontcolor|green|2}}, {{fontcolor|blue|1}}{{fontcolor|red|7}}, {{fontcolor|green|0}}, {{fontcolor|blue|6}}

|}

In anonymous games, players have different utilities but do not distinguish between other players (for instance, having to choose between "go to cinema" and "go to bar" while caring only how crowded will each place be, not who'll they meet there). In such a game a player's utility again depends on how many of his peers choose which strategy, and his own, so 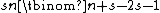utility values are required.

If the number of actions grows with the number of players, finding a pure Nash equilibrium in an anonymous game is NP-hard.[9] An optimal correlated equilibrium of an anonymous game may be found in polynomial time.[2] When the number of strategies is 2, there is a known PTAS for finding an ε-approximate Nash equilibrium.[14]

{{Clear}}

Polymatrix games

If the game in question was a polymatrix game, describing it would require 24 utility values. For simplicity, let us examine only the utilities of player I (we would need two more such tables for each of the other players).
            !align="center"|''L''            !align="center"|''R''
{{fontcolor|red|4}}, {{fontcolor|green|6}}{{fontcolor|red|8}}, {{fontcolor|green|7}}
{{fontcolor|red|3}}, {{fontcolor|green|7}}{{fontcolor|red|9}}, {{fontcolor|green|1}}

|
            !align="center"|''l''            !align="center"|''r''

|-
|align="center"|{{fontcolor|red|7}}, {{fontcolor|blue|7}}
|align="center"|{{fontcolor|red|1}}, {{fontcolor|blue|6}}
|-
|align="center"|{{fontcolor|red|8}}, {{fontcolor|blue|6}}
|align="center"|{{fontcolor|red|6}}, {{fontcolor|blue|4}}
|}
|
            !align="center"|''l''            !align="center"|''r''

|-
|align="center"|{{fontcolor|green|2}}, {{fontcolor|blue|9}}
|align="center"|{{fontcolor|green|3}}, {{fontcolor|blue|3}}
|-
|align="center"|{{fontcolor|green|2}}, {{fontcolor|blue|4}}
|align="center"|{{fontcolor|green|1}}, {{fontcolor|blue|5}}
|}

If strategy profile (B,R,l) was chosen, player I's utility would be 9+8=17, player II's utility would be 1+2=3, and player III's utility would be 6+4=10.


|}

In a polymatrix game (also known as a multimatrix game), there is a utility matrix for every pair of players (i,j), denoting a component of player i's utility. Player i's final utility is the sum of all such components. The number of utilities values required to represent such a game is .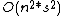

Polymatrix games always have at least one mixed Nash equilibrium.[15] The problem of finding a Nash equilibrium in a polymatrix game is PPAD-complete.[5] Moreover, the problem of finding a constant approximate Nash equilibrium in a polymatrix game is also PPAD-complete.[1] Finding a correlated equilibrium of a polymatrix game can be done in polynomial time.[2]

{{Clear}}

Circuit games

Let us now equate the players' various strategies with the Boolean values "0" and "1", and let X stand for player I's choice, Y for player II's choice and Z for player III's choice. Let us assign each player a circuit:

Player I: X ∧ (Y ∨ Z)

Player II: X ⨁ Y ⨁ Z

Player III: X ∨ Y

These describe the utility table below.

0, 00, 11, 01, 1
0{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|0}}{{fontcolor|red|0}}, {{fontcolor|green|1}}, {{fontcolor|blue|0}}{{fontcolor|red|0}}, {{fontcolor|green|1}}, {{fontcolor|blue|1}}{{fontcolor|red|0}}, {{fontcolor|green|0}}, {{fontcolor|blue|1}}
1{{fontcolor|red|0}}, {{fontcolor|green|1}}, {{fontcolor|blue|1}}{{fontcolor|red|1}}, {{fontcolor|green|0}}, {{fontcolor|blue|1}}{{fontcolor|red|1}}, {{fontcolor|green|0}}, {{fontcolor|blue|1}}{{fontcolor|red|1}}, {{fontcolor|green|1}}, {{fontcolor|blue|1}}

The most flexible of way of representing a succinct game is by representing each player by a polynomial-time bounded Turing machine, which takes as its input the actions of all players and outputs the player's utility. Such a Turing machine is equivalent to a Boolean circuit, and it is this representation, known as circuit games, that we will consider.

Computing the value of a 2-player zero-sum circuit game is an EXP-complete problem,[19] and approximating the value of such a game up to a multiplicative factor is known to be in PSPACE.[20] Determining whether a pure Nash equilibrium exists is a -complete problem (see Polynomial hierarchy).[21]

{{Clear}}

Other representations

Many other types of succinct game exist (many having to do with allocation of resources). Examples include congestion games, network congestion games, scheduling games, local effect games, facility location games, action-graph games, hypergraphical games and more.

Summary of complexities of finding equilibria

Below is a table of some known complexity results for finding certain classes of equilibria in several game representations. "NE" stands for "Nash equilibrium", and "CE" for "correlated equilibrium". n is the number of players and s is the number of strategies each player faces (we're assuming all players face the same number of strategies). In graphical games, d is the maximum indegree of the game graph. For references, see main article text.

Representation Size (O(...)) Pure NE Mixed NE CE Optimal CE
Normal form game 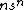NP-complete PPAD-complete P P
Graphical game 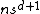NP-complete PPAD-complete P NP-hard
Symmetric game NP-complete The computation of symmetric Nash equilibrium is PPAD-hard for two players. The computation of non-symmetric Nash equilibrium for two players is NP-complete. P P
Anonymous game 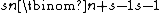NP-hard P P
Polymatrix game 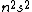PPAD-complete P NP-hard
Circuit game -complete
Congestion game PLS-complete P NP-hard

Notes

1. ^{{Cite book|last=Rubinstein|first=Aviad|date=2015-01-01|title=Inapproximability of Nash Equilibrium|journal=Proceedings of the Forty-seventh Annual ACM Symposium on Theory of Computing|series=STOC '15|location=New York, NY, USA|publisher=ACM|pages=409–418|doi=10.1145/2746539.2746578|isbn=9781450335362|arxiv=1405.3322}}
2. ^1  {{Cite book | pages = 262–273 | last1 = Chen | first1 = Xi | last2 = Deng | first2 = Xiaotie | last3 = Teng | first3 = Shang-Hua | title = Internet and Network Economics | chapter = Sparse Games Are Hard | year = 2006 | doi = 10.1007/11944874_24 | isbn = 978-3-540-68138-0 | chapterurl = http://www.springerlink.com/content/v2603131200h23hq/ }}
3. ^1  {{Cite journal | volume = 24 | issue = 195–220 | pages = 26–37 | last1 = Gottlob | first1 = G. | last2 = Greco | first2 = G. | last3 = Scarcello | first3 = F. | title = Pure Nash Equilibria: Hard and Easy Games | journal = Journal of Artificial Intelligence Research | year = 2005 | doi = 10.1613/jair.1683 }}
4. ^1  {{Cite conference | publisher = ACM | doi = 10.1145/1132516.1132526 | isbn = 1-59593-134-1 | pages = 61–70 | last1 = Goldberg | first1 = Paul W. | last2 = Papadimitriou | first2 = Christos H. | title = Reducibility Among Equilibrium Problems | booktitle = Proceedings of the thirty-eighth annual ACM symposium on Theory of computing | location = Seattle, WA, USA | accessdate = 2010-01-25 | year = 2006 | url = http://portal.acm.org/citation.cfm?id=1132516.1132526 }}
5. ^1  {{Cite journal | issn = 0025-1909 | volume = 18 | issue = 5 | pages = 312–318 | last = Howson | first = Joseph T. | title = Equilibria of Polymatrix Games | journal = Management Science|date=January 1972 | jstor = 2634798 | doi=10.1287/mnsc.18.5.312 }}
6. ^1 2 3 4 5  {{Cite journal | doi = 10.1145/1379759.1379762 | volume = 55 | issue = 3 | pages = 1–29 | last1 = Papadimitriou | first1 = Christos H. | last2 = Roughgarden | first2 = Tim | title = Computing Correlated Equilibria in Multi-Player Games | journal = J. ACM | year = 2008 | citeseerx = 10.1.1.335.2634 }}
7. ^1  {{Cite conference | conference = AAMAS-04 Workshop on Game Theory and Decision Theory | last1 = Cheng | first1 = Shih-Fen | last2 = Reeves | first2 = Daniel M. | last3 = Vorobeychik | first3 = Yevgeniy | last4 = Wellman | first4 = Michael P. | title = Notes on Equilibria in Symmetric Games | year = 2004 }}
8. ^1  {{Cite conference | publisher = Society for Industrial and Applied Mathematics | isbn = 0-89871-585-7 | pages = 82–91 | last1 = Papadimitriou | first1 = Christos H. | last2 = Roughgarden | first2 = Tim | title = Computing equilibria in multi-player games | booktitle = Proceedings of the sixteenth annual ACM-SIAM symposium on Discrete algorithms | location = Vancouver, British Columbia | accessdate = 2010-01-25 | year = 2005 | url = http://portal.acm.org/citation.cfm?id=1070432.1070444 }}
9. ^1  {{Cite arXiv | last1 = Daskalakis | first1 = Constantinos | last2 = Papadimitriou | first2 = Christos H. | eprint = 0710.5582v1 | class = cs | title = Computing Equilibria in Anonymous Games | year = 2007 }}
10. ^1 2  {{Cite book | pages = 513–524 | last1 = Daskalakis | first1 = Constantinos | last2 = Fabrikant | first2 = Alex | last3 = Papadimitriou | first3 = Christos H. | title = Automata, Languages and Programming | volume = 4051 | chapter = The Game World Is Flat: The Complexity of Nash Equilibria in Succinct Games| year = 2006 | doi = 10.1007/11786986_45 | series = Lecture Notes in Computer Science | isbn = 978-3-540-35904-3 | citeseerx = 10.1.1.111.8075 }}
11. ^1  {{Cite conference | publisher = Certer for Discrete Mathematics \\& Theoretical Computer Science | last1 = Feigenbaum | first1 = Joan | last2 = Koller | first2 = Daphne | last3 = Shor | first3 = Peter | title = A Game-Theoretic Classification of Interactive Complexity Classes | accessdate = 2010-01-25 | year = 1995 | url = http://portal.acm.org/citation.cfm?id=868345 }}
12. ^1  {{Cite conference | publisher = ACM | doi = 10.1145/1134707.1134737 | isbn = 1-59593-236-4 | pages = 270–279 | last1 = Schoenebeck | first1 = Grant | last2 = Vadhan | first2 = Salil | title = The computational complexity of nash equilibria in concisely represented games | booktitle = Proceedings of the 7th ACM conference on Electronic commerce | location = Ann Arbor, Michigan, USA | accessdate = 2010-01-25 | year = 2006 | url = http://portal.acm.org/citation.cfm?id=1134707.1134737 }}
13. ^1  {{Cite conference | publisher = IEEE Computer Society | isbn = 0-7695-2364-1 | pages = 323–332 | last1 = Fortnow | first1 = Lance | last2 = Impagliazzo | first2 = Russell | last3 = Kabanets | first3 = Valentine | last4 = Umans | first4 = Christopher | title = On the Complexity of Succinct Zero-Sum Games | booktitle = Proceedings of the 20th Annual IEEE Conference on Computational Complexity | accessdate = 2010-01-23 | year = 2005 | url = http://portal.acm.org/citation.cfm?id=1068661 }}
14. ^1 2  {{Cite journal | volume = 75 | issue = 3 | pages = 163–177 | last1 = Brandt | first1 = Felix | last2 = Fischer | first2 = Felix | last3 = Holzer | first3 = Markus | title = Symmetries and the Complexity of Pure Nash Equilibrium | journal = J. Comput. Syst. Sci. | accessdate = 2010-01-31 | year = 2009 | url = http://portal.acm.org/citation.cfm?id=1501295 | doi=10.1016/j.jcss.2008.09.001 }}
[2][3][4][5][6][7][8][9][10][11][12][13][14]
}}

External links

  • Algorithmic Game Theory: The Computational Complexity of Pure Nash
{{Game theory}}

1 : Game theory game classes
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/11 20:06:10