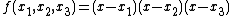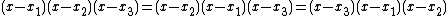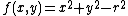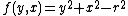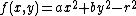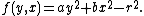“Symmetric function”的意思、由来-开放百科全书

词条

Symmetric function

释义

Symmetrization
Examples
Applications
U-statistics
See also
References

{{About|general properties of symmetric functions|the ring of symmetric functions in algebraic combinatorics|ring of symmetric functions}}

In mathematics, a symmetric function of n variables is one whose value given n arguments is the same no matter the order of the arguments. For example, if 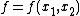is a symmetric function, then 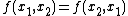for all pairs in the domain of . While this notion can apply to any type of function whose n arguments have the same domain set, it is most often used for polynomial functions, in which case these are the functions given by symmetric polynomials. There is very little systematic theory of symmetric non-polynomial functions of n variables, so this sense is little-used, except as a general definition.

Symmetrization

Given any function f in n variables with values in an abelian group, a symmetric function can be constructed by summing values of f over all permutations of the arguments. Similarly, an anti-symmetric function can be constructed by summing over even permutations and subtracting the sum over odd permutations. These operations are of course not invertible, and could well result in a function that is identically zero for nontrivial functions f. The only general case where f can be recovered if both its symmetrization and anti-symmetrization are known is when n = 2 and the abelian group admits a division by 2 (inverse of doubling); then f is equal to half the sum of its symmetrization and its anti-symmetrization.

Examples

Consider the real function

By definition, a symmetric function with n variables has the property that

etc.

In general, the function remains the same for every permutation of its variables. This means that, in this case,

and so on, for all permutations of

Consider the function

If x and y are interchanged the function becomes

which yields exactly the same results as the original f(x,y).

Consider now the function

If x and y are interchanged, the function becomes

This function is obviously not the same as the original if {{nowrap|1=a ≠ b}}, which makes it non-symmetric.

Applications

U-statistics

In statistics, an n-sample statistic (a function in n variables) that is obtained by bootstrapping symmetrization of a k-sample statistic, yielding a symmetric function in n variables, is called a U-statistic. Examples include the sample mean and sample variance.

References

F. N. David, M. G. Kendall & D. E. Barton (1966) Symmetric Function and Allied Tables, Cambridge University Press.
Joseph P. S. Kung, Gian-Carlo Rota, & Catherine H. Yan (2009) Combinatorics: The Rota Way, §5.1 Symmetric functions, pp 222–5, Cambridge University Press, {{isbn|978-0-521-73794-4}} .

2 : Symmetric functions|Combinatorics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Symmetrization

Examples

Applications

U-statistics

See also

References