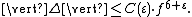“Szpiro's conjecture”的意思、由来-开放百科全书

词条

Szpiro's conjecture

释义

Statement
Modified Szpiro conjecture
References

{{Infobox mathematical statement
| name = Modified Szpiro conjecture
| image =
| caption =
| field = Number theory
| conjectured by = Lucien Szpiro
| conjecture date = 1981
| first proof by =
| first proof date =
| open problem =
| known cases =
| implied by
| equivalent to = abc conjecture
| generalizations =
| consequences = {{plainlist|

Beal conjecture
Faltings's theorem
Fermat's Last Theorem
Fermat–Catalan conjecture
Roth's theorem
Tijdeman's theorem}}

}}

In number theory, Szpiro's conjecture concerns a relationship between the conductor and the discriminant of an elliptic curve. In a general form, it is equivalent to the well-known abc conjecture. It is named for Lucien Szpiro who formulated it in the 1980s.

Statement

The conjecture states that: given ε > 0, there exists a constant C(ε) such that for any elliptic curve E defined over Q with minimal discriminant Δ and conductor f, we have

Modified Szpiro conjecture

The modified Szpiro conjecture states that: given ε > 0, there exists a constant C(ε) such that for any elliptic curve E defined over Q with invariants c₄, c₆ and conductor f (using notation from Tate's algorithm), we have

References

{{citation |first=S. |last=Lang |authorlink=Serge Lang |title=Survey of Diophantine geometry |publisher=Springer-Verlag |location=Berlin |year=1997 |isbn=3-540-61223-8 | zbl=0869.11051 | page=51 }}
{{citation |first=L. |last=Szpiro |title=Seminaire sur les pinceaux des courbes de genre au moins deux |journal=Astérisque |volume=86 |issue=3 |year=1981 | zbl=0463.00009 | pages=44–78 }}
{{citation |first=L. |last=Szpiro |title=Présentation de la théorie d'Arakelov |journal=Contemp. Math. |volume=67 |year=1987 | zbl=0634.14012 | pages=279–293 |doi=10.1090/conm/067/902599}}

2 : Conjectures|Number theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。