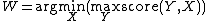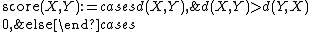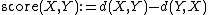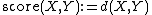- Description of the method Variants of the pairwise score
- Satisfied and failed criteria
- Examples Example with Condorcet winner Example with Condorcet winner that is not elected winner (for pairwise opposition) Example without Condorcet winner
- See also
- References
- External links
In voting systems, the minimax method is one of several Condorcet methods used for tabulating votes and determining a winner when using ranked voting in a single-winner election. It is also known as the Simpson–Kramer method, and the successive reversal method.
Minimax selects as the winner the candidate whose greatest pairwise defeat is smaller than the greatest pairwise defeat of any other candidate.
Description of the method
Minimax selects the candidate for whom the greatest pairwise score for another candidate against him or her is the least such score among all candidates.
Formally, let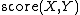 
denote the pairwise score for 
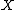against 
.
Then the candidate, 
selected by minimax (aka the winner) is given by:
Variants of the pairwise score
When it is permitted to rank candidates equally, or to not rank all the candidates, three interpretations of the rule are possible. When voters must rank all the candidates, all three variants are equivalent.
Let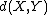 
be the number of voters ranking X over Y. The variants define the score 
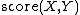for candidate X against Y as:
- The number of voters ranking X above Y, but only when this score exceeds the number of voters ranking Y above X. If not, then the score for X against Y is zero. This variant is sometimes called winning votes.
- The number of voters ranking X above Y minus the number of voters ranking Y above X. This variant is called using margins.
- The number of voters ranking X above Y, regardless of whether more voters rank X above Y or vice versa. This variant is sometimes called pairwise opposition.
When one of the first two variants is used, the method can be restated as: "Disregard the weakest pairwise defeat until one candidate is unbeaten." An "unbeaten" candidate possesses a maximum score against him which is zero or negative.
Satisfied and failed criteria
Minimax using winning votes or margins satisfies the Condorcet and the majority criterion, but not the Smith criterion, mutual majority criterion, independence of clones criterion, or Condorcet loser criterion. When winning votes is used, minimax also satisfies the Plurality criterion.
When the pairwise opposition variant is used, minimax also does not satisfy the Condorcet criterion. However, when equal-ranking is permitted, there is never an incentive to put one's first-choice candidate below another one on one's ranking. It also satisfies the later-no-harm criterion, which means that by listing additional, lower preferences in one's ranking, one cannot cause a preferred candidate to lose.
Examples
Example with Condorcet winner
{{Tenn voting example}}The results of the pairwise scores would be tabulated as follows:
| X | |||||
| Memphis | Nashville | Chattanooga | Knoxville | ||
| Y | Memphis | [X] 58% [Y] 42% | [X] 58% [Y] 42% | [X] 58% [Y] 42% | |
| Nashville | [X] 42% [Y] 58% | [X] 32% [Y] 68% | [X] 32% [Y] 68% | ||
| Chattanooga | [X] 42% [Y] 58% | [X] 68% [Y] 32% | [X] 17% [Y] 83% | ||
| Knoxville | [X] 42% [Y] 58% | [X] 68% [Y] 32% | [X] 83% [Y] 17% | ||
| Pairwise election results (won-tied-lost): | 0-0-3 | 3-0-0 | 2-0-1 | 1-0-2 | |
| worst pairwise defeat (winning votes): | 58% | 0% | 68% | 83% | |
| worst pairwise defeat (margins): | 16% | −16% | 36% | 66% | |
| worst pairwise opposition: | 58% | 42% | 68% | 83% | |
- [X] indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
- [Y] indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption
Result: In all three alternatives Nashville, the capital in real life, has the lowest value and is elected winner.
Example with Condorcet winner that is not elected winner (for pairwise opposition)
Assume three candidates A, B and C and voters with the following preferences:
| 4% of voters | 47% of voters | 43% of voters | 6% of voters |
|---|---|---|---|
| 1. A and C | 1. A | 1. C | 1. B |
| 2. C | 2. B | 2. A and C | |
| 3. B | 3. B | 3. A |
The results would be tabulated as follows:
| X | ||||
| A | B | C | ||
| Y | A | [X] 49% [Y] 51% | [X] 43% [Y] 47% | |
| B | [X] 51% [Y] 49% | [X] 94% [Y] 6% | ||
| C | [X] 47% [Y] 43% | [X] 6% [Y] 94% | ||
| Pairwise election results (won-tied-lost): | 2-0-0 | 0-0-2 | 1-0-1 | |
| worst pairwise defeat (winning votes): | 0% | 94% | 47% | |
| worst pairwise defeat (margins): | −2% | 88% | 4% | |
| worst pairwise opposition: | 49% | 94% | 47% | |
- [X] indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
- [Y] indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption
Result: With the alternatives winning votes and margins, the Condorcet winner A is declared Minimax winner. However, using the pairwise opposition alternative, C is declared winner, since less voters strongly oppose him in his worst pairwise score against A than A is opposed by in his worst pairwise score against B.
Example without Condorcet winner
Assume four candidates A, B, C and D. Voters are allowed to not consider some candidates (denoting an n/a in the table), so that their ballots are not taken into account for pairwise scores of that candidates.
| 30 voters | 15 voters | 14 voters | 6 voters | 4 voters | 16 voters | 14 voters | 3 voters |
|---|---|---|---|---|---|---|---|
| 1. A | 1. D | 1. D | 1. B | 1. D | 1. C | 1. B | 1. C |
| 2. C | 2. B | 2. B | 2. C | 2. C | 2. A and B | 2. C | 2. A |
| 3. B | 3. A | 3. C | 3. A | 3. A and B | |||
| 4. D | 4. C | 4. A | 4. D | ||||
| n/a D | n/a A and D | n/a B and D | |||||
The results would be tabulated as follows:
| X | |||||
| A | B | C | D | ||
| Y | A | [X] 35 [Y] 30 | [X] 43 [Y] 45 | [X] 33 [Y] 36 | |
| B | [X] 30 [Y] 35 | [X] 50 [Y] 49 | [X] 33 [Y] 36 | ||
| C | [X] 45 [Y] 43 | [X] 49 [Y] 50 | [X] 33 [Y] 36 | ||
| D | [X] 36 [Y] 33 | [X] 36 [Y] 33 | [X] 36 [Y] 33 | ||
| Pairwise election results (won-tied-lost): | 2-0-1 | 2-0-1 | 2-0-1 | 0-0-3 | |
| worst pairwise defeat (winning votes): | 35 | 50 | 45 | 36 | |
| worst pairwise defeat (margins): | 5 | 1 | 2 | 3 | |
| worst pairwise opposition: | 43 | 50 | 49 | 36 | |
- [X] indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
- [Y] indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption
Result:
Each of the three alternatives gives another winner:
- the winning votes alternative chooses A as winner, since it has the lowest value of 35 votes for the winner in his biggest defeat;
- the margin alternative chooses B as winner, since it has the lowest difference of votes in his biggest defeat;
- and pairwise opposition chooses the Condorcet loser D as winner, since it has the lowest votes of the biggest opponent in all pairwise scores.
See also
- Minimax – main minimax article
- Wald's maximin model – Wald's maximin model
References
- Levin, Jonathan, and Barry Nalebuff. 1995. "An Introduction to Vote-Counting Schemes." Journal of Economic Perspectives, 9(1): 3–26.
External links
- Description of ranked ballot voting methods: Simpson by Rob LeGrand
- [https://github.com/julien-boudry/Condorcet_Schulze-PHP_Class Condorcet Class] PHP library supporting multiple Condorcet methods, including the three variants of Minimax method.
- [https://electowiki.org/wiki/Minmax Electowiki: minmax]
- Pirámides railway station
- Pirá-Tapuya
- Piré-Chancé
- P.I.S.A.
- PISA 2015
- Pisa Aeroporto
- Pisa Aeroporto station
- Pisa (airport)
- Pisa Altarpiece
- Pisa Baptistry
- Pisaboa
- Pisacayo
- Pisaccacunca
- Pisachas
- Pisa chronology
- Pisa Foundation
- Pisagua prison camp
- Pisagua Prison Camp
- Pisagua Prisoner-of-war camp
- Pisagua prisoner-of-war camp
- PISAI
- Pisa International
- Pisa International (airport)
- Pisa (international airport)
- Pisamira