1. Zero-sum Games

2. See also

3. References

A minimax theorem is a theorem providing conditions that guarantee that the max–min inequality is also an equality.

The first theorem in this sense is von Neumann's minimax theorem from 1928, which was considered the starting point of game theory.

Since then, several generalizations and alternative versions of von Neumann's original theorem have appeared in the literature.^[1][2]

Zero-sum Games

The minimax theorem was first proven and published in 1928 by John von Neumann,^[3] who is quoted as saying "As far as I can see, there could be no theory of games … without that theorem … I thought there was nothing worth publishing until the Minimax Theorem was proved".^[4]

Formally, von Neumann's minimax theorem states:

Let 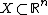and 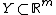be compact convex sets. If 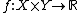is a continuous function that is convex-concave, i.e.

is convex for fixed , and

is concave for fixed .

Then we have that

See also

• Sion's minimax theorem
• Parthasarathy's theorem
• Dual linear program can be used to prove the minimax theorem for zero-sum games.

References

• Gnaphalium sphacelatum
• Gnaphalium sphacilatum
• Gnaphalium sphaericum
• Gnaphalium stachidifolium
• Gnaphalium stachydifolium
• Gnaphalium stagnale
• Gnaphalium stenophyllum
• Gnaphalium strictum
• Gnaphalium timmua
• Gnaphalium tomentosum
• Gnaphalium tunariense
• Gnaphalium uniflorum
• Gnaphalium ustulatum
• Gnaphalium wightianum
• Gnaphalium wirtgenii
• Gnaphalium yedoense
• Gnaphalodes
• Gnaphalodes condensata
• Gnaphalodes evacinum
• Gnaphalon
• Gnaphalopsis
• Gnaphalostoma nivacula
• Gnaphon
• Gnaphosa
• Gnaphosa alacris