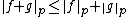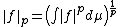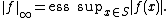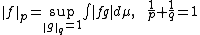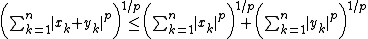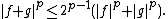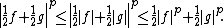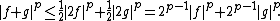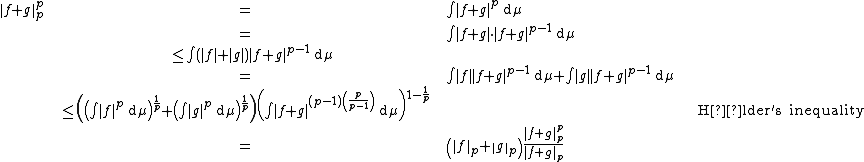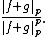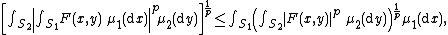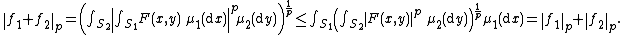“Minkowski inequality”的意思、由来-开放百科全书

词条

Minkowski inequality

释义

Proof
Minkowski's integral inequality
See also
References

{{hatnote|This page is about Minkowski's inequality for norms. See Minkowski's first inequality for convex bodies for Minkowski's inequality in convex geometry.}}

In mathematical analysis, the Minkowski inequality establishes that the L^p spaces are normed vector spaces. Let S be a measure space, let {{nowrap|1 ≤ p ≤ ∞}} and let f and g be elements of L^p(S). Then {{nowrap|f + g}} is in L^p(S), and we have the triangle inequality

with equality for {{nowrap|1 < p < ∞}} if and only if f and g are positively linearly dependent, i.e., {{nowrap|1=f = λg}} for some {{nowrap|λ ≥ 0}} or {{nowrap|1=g = 0}}. Here, the norm is given by:

if p < ∞, or in the case p = ∞ by the essential supremum

The Minkowski inequality is the triangle inequality in L^p(S). In fact, it is a special case of the more general fact

where it is easy to see that the right-hand side satisfies the triangular inequality.

Like Hölder's inequality, the Minkowski inequality can be specialized to sequences and vectors by using the counting measure:

for all real (or complex) numbers x₁, ..., x_n, y₁, ..., y_n and where n is the cardinality of S (the number of elements in S).

Proof

First, we prove that f+g has finite p-norm if f and g both do, which follows by

Indeed, here we use the fact that 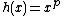is convex over {{math|R⁺}} (for {{math|p > 1}}) and so, by the definition of convexity,

This means that

Now, we can legitimately talk about 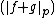. If it is zero, then Minkowski's inequality holds. We now assume that 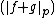is not zero. Using the triangle inequality and then Hölder's inequality, we find that

We obtain Minkowski's inequality by multiplying both sides by

Minkowski's integral inequality

Suppose that {{nowrap|(S₁, μ₁)}} and {{nowrap|(S₂, μ₂)}} are two σ-finite measure spaces and {{nowrap|F′ : S₁ × S₂ → R}} is measurable. Then Minkowski's integral inequality is {{harv|Stein|1970|loc=§A.1}}, {{harv|Hardy|Littlewood|Pólya|1988|loc=Theorem 202}}:

with obvious modifications in the case {{nowrap|1=p = ∞}}. If {{nowrap|p > 1}}, and both sides are finite, then equality holds only if {{nowrap|1={{abs|F(x, y)}} = φ(x)ψ(y)}} a.e. for some non-negative measurable functions φ and ψ.

If μ₁ is the counting measure on a two-point set {{nowrap|1=S₁ = {1,2},}} then Minkowski's integral inequality gives the usual Minkowski inequality as a special case: for putting {{nowrap|1=f_i(y) = F(i, y)}} for {{nowrap|1=i = 1, 2}}, the integral inequality gives

References

{{Cite book|last1=Hardy|first1=G. H.|author1-link=G. H. Hardy|last2=Littlewood|first2=J. E.|author2-link=John Edensor Littlewood|last3= Pólya| first3 = G.| author3-link = George Pólya| title = Inequalities|series = Cambridge Mathematical Library| edition = second| publisher = Cambridge University Press| location = Cambridge| year = 1952|isbn = 0-521-35880-9}}
{{Cite journal|first=H.|last=Minkowski|authorlink=Hermann Minkowski|title=Geometrie der Zahlen| publisher=Chelsea |year=1953 |ref=harv| postscript={{inconsistent citations}}}}.
{{Cite journal|first=Elias|last=Stein|authorlink=Elias Stein|title=Singular integrals and differentiability properties of functions|publisher=Princeton University Press|year=1970|ref=harv|postscript={{inconsistent citations}}}}.
{{springer|id=M/m064060|title=Minkowski inequality|author=M.I. Voitsekhovskii}}
{{cite web|title=Introduction to Inequalities|url= |author=Arthur Lohwater|year=1982}}

3 : Inequalities|Articles containing proofs|Measure theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Proof

Minkowski's integral inequality

See also

References