“Tangent indicatrix”的意思、由来-开放百科全书

词条

Tangent indicatrix

释义

References

In differential geometry, the tangent indicatrix of a closed space curve is a curve on the unit sphere intimately related to the curvature of the original curve. Let be a closed curve with nowhere-vanishing tangent vector 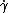. Then the tangent indicatrix of is the closed curve on the unit sphere given by .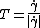

The total curvature of (the integral of curvature with respect to arc length along the curve) is equal to the arc length of .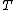

References

Solomon, B. "Tantrices of Spherical Curves." Amer. Math. Monthly 103, 30-39, 1996.

2 : Differential geometry|Spherical geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。