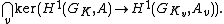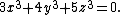“Tate–Shafarevich group”的意思、由来-开放百科全书

词条

Tate–Shafarevich group

释义

Elements of the Tate–Shafarevich group
Shafarevich–Tate conjecture
Cassels–Tate pairing
See also
References

In arithmetic geometry, the Tate–Shafarevich group Ш(A/K), introduced by {{harvs|txt|last1=Lang|first1=Serge|authorlink1=Serge Lang|author2-link=John Tate|last2=Tate|first2=John|year=1958}} and {{harvs|txt|authorlink=Igor Shafarevich|last=Shafarevich|first=Igor|year=1959}}, of an abelian variety A (or more generally a group scheme) defined over a number field K consists of the elements of the Weil–Châtelet group WC(A/K) = H¹(G_K, A) that become trivial in all of the completions of K (i.e. the p-adic fields obtained from K, as well as its real and complex completions). Thus, in terms of Galois cohomology, it can be written as

{{quote box|align=right|width=33%
|quote=This is the author's most lasting contribution to the subject. The original notation was TS, which, Tate tells me, was intended to continue the lavatorial allusion of WC. The Americanism "tough shit" indicates the part that is difficult to eliminate.
|source={{harvs|txt|last=Cassels|first=J. W. S.|authorlink=J. W. S. Cassels|year=1990|loc=footnote on page 109}}, commenting on his introduction of the notation Ш.}}

Cassels introduced the notation Ш(A/K), where Ш is the Cyrillic letter "Sha", for Shafarevich, replacing the older notation TS.

Elements of the Tate–Shafarevich group

Geometrically, the non-trivial elements of the Tate–Shafarevich group can be thought of as the homogeneous spaces of A that have K_v-rational points for every place v of K, but no K-rational point. Thus, the group measures the extent to which the Hasse principle fails to hold for rational equations with coefficients in the field K. {{harvs|txt|last=Lind|first=Carl-Erik|year=1940}} gave an example of such a homogeneous space, by showing that the genus 1 curve

has solutions over the reals and over all p-adic fields, but has no rational points.

{{harvs|txt|last=Selmer|first=Ernst S.|authorlink=Ernst Sejersted Selmer|year=1951}} gave many more examples, such as

The special case of the Tate–Shafarevich group for the finite group scheme consisting of points of some given finite order n of an abelian variety is closely related to the Selmer group.

Shafarevich–Tate conjecture

The Tate–Shafarevich conjecture states that the Tate–Shafarevich group is finite. {{harvs|txt|authorlink=Karl Rubin|last=Rubin|first=Karl|year=1987}} proved this for some elliptic curves of rank at most 1 with complex multiplication. {{harvs|txt|last=Kolyvagin|first=Victor A.|year=1988}} extended this to modular elliptic curves over the rationals of analytic rank at most 1. (The modularity theorem later showed that the modularity assumption always holds.)

Cassels–Tate pairing

The Cassels–Tate pairing is a bilinear pairing Ш(A)×Ш(Â)→Q/Z, where A is an abelian variety and Â is its dual.

{{harvtxt|Cassels|1962}} introduced this for elliptic curves, when A can be identified with Â and the pairing is an alternating form. The kernel of this form is the subgroup of divisible elements, which is trivial if the Tate–Shafarevich conjecture is true. {{harvtxt|Tate|1963}} extended the pairing to general abelian varieties, as a variation of Tate duality. A choice of polarization on A gives a map from A to Â, which induces a bilinear pairing on Ш(A) with values in Q/Z, but unlike the case of elliptic curves this need not be alternating or even skew symmetric.

For an elliptic curve, Cassels showed that the pairing is alternating, and a consequence is that if the order of Ш is finite then it is a square. For more general abelian varieties it was sometimes incorrectly believed for many years that the order of Ш is a square whenever it is finite; this mistake originated in a paper by {{harvtxt|Swinnerton-Dyer|1967}}, who misquoted one of the results of {{harvtxt|Tate|1963}}. {{harvtxt|Poonen|Stoll|1999}} gave some examples where the order is twice a square, such as the Jacobian of a certain genus 2 curve over the rationals whose Tate–Shafarevich group has order 2, and {{harvtxt|Stein|2004}} gave some examples where the power of an odd prime dividing the order is odd. If the abelian variety has a principal polarization then the form on Ш is skew symmetric which implies that the order of Ш is a square or twice a square (if it is finite), and if in addition the principal polarization comes from a rational divisor (as is the case for elliptic curves) then the form is alternating and the order of Ш is a square (if it is finite).

References

{{Citation | last1=Cassels | first1=John William Scott | title=Arithmetic on curves of genus 1. III. The Tate–Šafarevič and Selmer groups | doi=10.1112/plms/s3-12.1.259 |mr=0163913 | year=1962 | journal=Proceedings of the London Mathematical Society |series=Third Series | issn=0024-6115 | volume=12 | pages=259–296}}
{{Citation | last1=Cassels | first1=John William Scott | title=Arithmetic on curves of genus 1. IV. Proof of the Hauptvermutung | url=http://resolver.sub.uni-goettingen.de/purl?GDZPPN002179873 |mr=0163915 | year=1962b | journal=Journal für die reine und angewandte Mathematik | issn=0075-4102 | volume=211 | issue=211 | pages=95–112 | doi=10.1515/crll.1962.211.95}}
{{Citation | last1=Cassels | first1=John William Scott | title=Lectures on elliptic curves | url=https://books.google.com/books?id=zgqUAuEJNJ4C | publisher=Cambridge University Press | series=London Mathematical Society Student Texts | isbn=978-0-521-41517-0 |mr=1144763 | year=1991 | volume=24 | doi=10.1017/CBO9781139172530}}
{{Citation | last2=Silverman | first2=Joseph H. | author2-link=Joseph H. Silverman | last1=Hindry | first1=Marc | author1-link=Marc Hindry | title=Diophantine geometry: an introduction | publisher=Springer-Verlag | location=Berlin, New York | series=Graduate Texts in Mathematics | isbn=978-0-387-98981-5 | year=2000 | volume=201}}
{{Citation | last1=Greenberg | first1=Ralph | author1-link=Ralph Greenberg | editor1-last=Serre | editor1-first=Jean-Pierre | editor1-link=Jean-Pierre Serre | editor2-last=Jannsen | editor2-first=Uwe | editor3-last=Kleiman | editor3-first=Steven L. | title=Motives | publisher=American Mathematical Society | location=Providence, R.I. | isbn=978-0-8218-1637-0 | year=1994 | chapter=Iwasawa Theory and p-adic Deformation of Motives}}
{{Citation | last1=Kolyvagin | first1=V. A. | title=Finiteness of E(Q) and SH(E,Q) for a subclass of Weil curves | id=954295 | year=1988 | journal=Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya | issn=0373-2436 | volume=52 | issue=3 | pages=522–540, 670–671}}
{{Citation | last1=Lang | first1=Serge | author1-link=Serge Lang | last2=Tate | first2=John | author2-link=John Tate | title=Principal homogeneous spaces over abelian varieties |mr=0106226 | year=1958 | journal=American Journal of Mathematics | issn=0002-9327 | volume=80 | issue=3 | pages=659–684 | doi=10.2307/2372778 | jstor=2372778}}
{{Cite thesis | last1=Lind | first1=Carl-Erik | title=Untersuchungen über die rationalen Punkte der ebenen kubischen Kurven vom Geschlecht Eins | url=https://books.google.com/books?id=ZggUAQAAIAAJ |mr=0022563 | year=1940 | publisher= University of Uppsala | volume=1940 | pages=97 pp.| nopp = y}}
{{Citation | last1=Poonen | first1=Bjorn | last2=Stoll | first2=Michael | title=The Cassels-Tate pairing on polarized abelian varieties | doi=10.2307/121064 |mr=1740984 | year=1999 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=150 | issue=3 | pages=1109–1149| arxiv=math/9911267 | jstor=121064 }}
{{Citation | last1=Rubin | first1=Karl | title=Tate-Shafarevich groups and L-functions of elliptic curves with complex multiplication | doi=10.1007/BF01388984 |mr=903383 | year=1987 | journal=Inventiones Mathematicae | issn=0020-9910 | volume=89 | issue=3 | pages=527–559| bibcode=1987InMat..89..527R }}
{{Citation | last1=Selmer | first1=Ernst S. | title=The Diophantine equation ax³+by³+cz³=0 | doi=10.1007/BF02395746 |mr=0041871 | year=1951 | journal=Acta Mathematica | issn=0001-5962 | volume=85 | pages=203–362 }}
{{Citation | last1=Shafarevich | first1=I. R. | title=The group of principal homogeneous algebraic manifolds | language=Russian |mr=0106227| year=1959 | journal=Doklady Akademii Nauk SSSR | issn=0002-3264 | volume=124 | pages=42–43}} English translation in his collected mathematical papers
{{Citation | last1=Stein | first1=William A. | title=Modular curves and abelian varieties | chapter-url=http://wstein.org/papers/nonsquaresha/final2.pdf | publisher=Birkhäuser | location=Basel, Boston, Berlin | series=Progr. Math. |mr=2058655 | year=2004 | volume=224 | chapter=Shafarevich-Tate groups of nonsquare order | pages=277–289}}
{{Citation | last1=Swinnerton-Dyer | first1=P. | editor1-last=Springer | editor1-first=Tonny A. | title=Proceedings of a Conference on Local Fields (Driebergen, 1966) | chapter-url=https://books.google.com/books/?id=I983HAAACAAJ | publisher=Springer-Verlag | location=Berlin, New York |mr=0230727 | year=1967 | chapter=The conjectures of Birch and Swinnerton-Dyer, and of Tate | pages=132–157}}
{{Citation | last1=Tate | first1=John | author1-link=John Tate | title=WC-groups over p-adic fields | url=http://www.numdam.org/item?id=SB_1956-1958__4__265_0 | publisher=Secrétariat Mathématique | location=Paris | series=Séminaire Bourbaki; 10e année: 1957/1958 |mr=0105420 | year=1958 | volume=13}}
{{Citation | last1=Tate | first1=John | author1-link=John Tate | title=Proceedings of the International Congress of Mathematicians (Stockholm, 1962) | chapter-url=http://mathunion.org/ICM/ICM1962.1/ | publisher=Inst. Mittag-Leffler | location=Djursholm | mr=0175892 | year=1963 | chapter=Duality theorems in Galois cohomology over number fields | pages=288–295 | deadurl=yes | archiveurl=https://web.archive.org/web/20110717144510/http://mathunion.org/ICM/ICM1962.1/ | archivedate=2011-07-17 | df= }}
{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=On algebraic groups and homogeneous spaces |mr=0074084 | year=1955 | journal=American Journal of Mathematics | issn=0002-9327 | volume=77 | issue=3 | pages=493–512 | doi=10.2307/2372637 | jstor=2372637}}

1 : Number theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Elements of the Tate–Shafarevich group

Shafarevich–Tate conjecture

Cassels–Tate pairing

See also

References