- Overview An example: Maybe Definition Usage
- Applications
- History
- Analysis Verifying the monad laws Derivation from functors Another example: List
- Techniques Syntax Sugar General interface Operators
- Variations Additive monads Free monads Comonads
- More examples Identity monad Collections I/O monad (Haskell) Writer monad (Javascript) Environment monad State monads Continuation monad
- See also
- Notes
- References
- External links
In functional programming, a monad is a design pattern[1] that allows structuring programs generically while automating away boilerplate code needed by the program logic.
Monads achieve this by providing their own data type, which represents a specific form of computation, along with one procedure to wrap values of any basic type within the monad (yielding a monadic value) and another to compose functions that output monadic values (called monadic functions).[2]
This allows monads to simplify a wide range of problems, like handling potential undefined values (with the Maybe monad), or keeping values within a flexible, well-formed list (using the List monad).
With a monad, a programmer can turn a complicated sequence of functions into a succinct pipeline that abstracts away auxiliary data management, control flow, or side-effects.[2][3]
Both the concept of a monad and the term originally come from category theory, where it is defined as a functor with additional structure.{{efn|Due to the fact that functions on multiple free variables are common in programming, monads as described in this article are technically what category theorists would call strong monads.[5]}}
Research beginning in the late 1980s and early 1990s established that monads could bring seemingly disparate computer-science problems under a unified, functional model.
Category theory also provides a few formal requirements, known as the monad laws, which should be satisfied by any monad and can be used to verify monadic code.[4][5]
Since monads make semantics explicit for a kind of computation, they can also be used to implement convenient language features.
Some languages, such as Haskell, even offer pre-built definitions in their core libraries for the general monad structure and common instances.[2][6]
Overview
"For a monad m, a value of type m a represents having access to a value of type a within the context of the monad." —C. A. McCann[7]
An example: Maybe
To motivate how and why to program with monads, a quick example in Haskell is provided here.
Undefined values or operations are one particular problem that robust software should prepare for and handle gracefully.
The first step towards this goal might be to create an option type that will mark a value as either of type T (T can be any type) or undefined. In Haskell the new type will be called Maybe T and can contain either a value of type T, or an undefined value Nothing.
Values of type T which are defined but used in the context of Maybe will be called Just T. This is done to avoid confusion by differentiating between variables which were tested to be defined and such which were not.
newtype Maybe T = Just T or Nothing
Maybe and Just can be understood as "wrapping" types, wrapping T type into a new type with built-in exception handling.
Another improvement would be if a function could manage simple checked exceptions with a Maybe type, short-circuiting and returning Nothing once a step fails, but returning the correct value without comment if a calculation succeeds.
The following code will add letters in front of variables to express their monad type. Take a variable x with the type T. mx will represent x with the type Maybe T while λx will be x of type Just T.
An addition function add, which does exactly this when adding two Maybe variables, mx and my, can be defined like so:
add(mx,my) = ... if mx is Nothing then ... Nothing else if my is Nothing then ... Nothing else ... Just (x + y) end if
Writing functions that process Maybe values case-by-case can be tedious though, and will only become more-so as more functions are defined.
An operation to chain steps together is one way to alleviate this, and with an infix operator like x >>= y, it can even intuitively represent feeding the (possibly undefined) result from each step into the next.
Since each result is technically inserted into another function, however, the operator will take a function for a parameter.
As add already specifies the type of its output value, it should not hurt to keep the operator flexible and accept functions that output different types from their input:
(mx >>= f) = ... if mx is (Just x) then ... f(x) -- f returns a defined value of type Maybe U else ... Nothing -- f returns undefined end if
With >>= available, add can now be redefined as something much more compact:
This is more concise, but a little extra analysis reveals something even more powerful.
For one, add only requires Just to tag an underlying value as also being a Maybe value.
To emphasize how Just acts on the underlying value by wrapping it, it can be redefined as a function too, called eta for now:
The big picture is that these two functions >>= and eta were designed to simplify add, but they clearly do not depend on the specifics of add in any way, just the Maybe type.
These functions can, in fact, apply to any values and functions of the Maybe type, regardless of the underlying values' types.
For example, here is a concise NOT operator from (Kleene's) trinary logic that uses the same functions to automate undefined values too:
trinot(mp) = mp >>= λp -> (eta ∘ not) p
It turns out the Maybe type, together with >>= and eta, forms a monad.
While other monads will embody different logical processes, and some may have extra properties, all of them will have three similar components (directly or indirectly) that follow the basic outline of this example.[2][8]
Definition
The more common definition for a monad in functional programming, used in the above example, is actually based on a Kleisli triple rather than category-theory's standard definition.
The two constructs turn out to be mathematically equivalent, however, so either definition will yield a valid monad.
Given any well-defined, basic types {{mvar|T,U}}, a monad consists of three parts:
- A type constructor {{mvar|M}} that builds up a monadic type {{mvar|M T}}{{efn|Semantically, {{mvar|M}} is not trivial and represents an endofunctor over the category of all well-typed values:
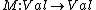 }}
}} - A type converter, often called unit or return, that embeds an object {{mvar|x}} in the monad:
unit(x) : T → M T{{efn|While a function in programming terms, {{mvar|unit}} (often called {{mvar|η}} in category-theory) is mathematically a natural transformation, which maps between functors:}}
- {{anchor|Bind}} A combinator, typically called bind (as in binding a variable) and represented with an infix operator
>>=, that unwraps a monadic variable, then inserts it into a monadic function/expression, resulting in a new monadic value:
{{anchor|Monad laws}}(mx >>= f) : (M T, T → M U) → M U{{efn|{{mvar|bind}}, on the other hand, is not a natural transformation in category theory, but rather an extensionthat lifts a mapping (from values to computations) into a morphism between computations:
}}
To fully qualify as a monad though, these three parts must also respect a few laws:
- {{mvar|unit}} is a left-identity for {{mvar|bind}}:
unit(a) >>= λx -> f(x) ↔ f(a)
- {{mvar|unit}} is also a right-identity for {{mvar|bind}}:
ma >>= λx -> unit(x) ↔ ma
- {{mvar|bind}} is essentially associative:{{efn|Strictly speaking, {{mvar|bind}} may not be formally associative in all contexts because it corresponds to application within lambda calculus, not mathematics. In rigorous lambda-calculus, evaluating a {{mvar|bind}} may require first wrapping the right term (when binding two monadic values) or the bind itself (between two monadic functions) in an anonymous function to still accept input from the left.[9]}}
ma >>= (λx -> f(x) >>= λy -> g(y)) ↔ (ma >>= λx -> f(x)) >>= λy -> g(y)[2]
Algebraically, this means any monad is both a category in its own right and a monoid in the category of functors (from values to computations), with monadic composition as a binary operator and {{mvar|unit}} as identity.{{citation needed|reason=Follows from the math and is a cliche, but should be somewhere in one of the sources|date=November 2018}}
Usage
The value of the monad pattern goes beyond merely condensing code and providing a link to mathematical reasoning.
Whatever language or default programming paradigm a developer uses, following the monad pattern brings many of the benefits of purely functional programming.
By reifying a specific kind of computation, a monad not only encapsulates the tedious details of that computational pattern, but it does so in a declarative way, improving the code's clarity.
As monadic values explicitly represent not only computed values, but computed effects, a monadic expression can be substituted with its value in referentially transparent positions, much like pure expressions can be, allowing for many techniques and optimizations based on rewriting.[5]
Typically, programmers will use {{mvar|bind}} to chain monadic functions into a sequence, which has led some to describe monads as "programmable semicolons", a reference to how many imperative languages use semicolons to separate statements.[2][6]
However, it should be stressed that monads do not actually order computations; even in languages that use them as central features, simpler function composition can arrange steps within a program.
A monad's general utility rather lies in simplifying a program's structure and improving separation of concerns through abstraction.[5][10]
The monad structure can also be seen as a uniquely mathematical and compile time variation on the decorator pattern.
Some monads can pass along extra data that is inaccessible to functions, and some even exert finer control over execution, for example only calling a function under certain conditions.
Because they let application programmers implement domain logic while offloading boilerplate code onto pre-developed modules, monads can even be considered a tool for aspect-oriented programming.[11]
One other noteworthy use for monads is isolating side-effects, like input/output or mutable state, in otherwise purely functional code.
Even purely functional languages can still implement these "impure" computations without monads, via an intricate mix of function composition and continuation-passing style (CPS) in particular.[3]
With monads though, much of this scaffolding can be abstracted away, essentially by taking each recurring pattern in CPS code and bundling it into a distinct monad.[5]
If a language does not support monads by default, it is still possible to implement the pattern, often without much difficulty.
When translated from category-theory to programming terms, the monad structure is a generic concept and can be defined directly in any language that supports an equivalent feature for bounded polymorphism.
A concept's ability to remain agnostic about operational details while working on underlying types is powerful, but the unique features and stringent behavior of monads set them apart from other concepts.[12]
Applications
Discussions of specific monads will typically focus on solving a narrow implementation problem since a given monad represents a specific computational form.
In some situations though, an application can even meet its high-level goals by using appropriate monads within its core logic.
Here are just a few applications that have monads at the heart of their designs:
- The Parsec parser library uses monads to combine simpler parsing rules into more complex ones, and is particularly useful for smaller domain-specific languages.[13]
- xmonad is a tiling window manager centered on the zipper data structure, which itself can be treated monadically as a specific case of delimited continuations.[14]
- LINQ by Microsoft provides a query language for the .NET Framework that is heavily influenced by functional programming concepts, including core operators for composing queries monadically.[15]
- ZipperFS is a simple, experimental file system that also uses the zipper structure primarily to implement its features.{{citation needed|reason=Sources are relatively easy to find by surfing / googling, but not sure which would be best|date=November 2018}}
- The Reactive extensions framework essentially provides a (co)monadic interface to data streams that realizes the observer pattern.[16]
History
The term "monad" in programming actually goes all the way back to the APL and J programming languages, which do tend toward being purely functional.
However, in those languages, "monad" is only shorthand for a function taking one parameter (a function with two parameters being a "dyad", and so on).[17]
The mathematician Roger Godement was the first to formulate the concept of a monad (dubbing it a "standard construction") in the late 1950s, though the term "monad" that came to dominate is due to category-theorist Saunders Mac Lane.{{Citation needed|reason=Don't have a copy of Mac Lane's book right now, but that could probably work as a source here|date=October 2018}}
The form defined above using {{mvar|bind}}, however, was originally described in 1965 by mathematician Heinrich Kleisli in order to prove that any monad could be characterized as an adjunction between two (covariant) functors.[18]
Starting in the 1980s, a vague notion of the monad pattern began to surface in the computer science community.
According to programming language researcher Philip Wadler, computer scientist John C. Reynolds anticipated several facets of it in the 70s and early 80s, when he discussed the value of continuation-passing style, category theory as a rich source for formal semantics, and the type distinction between values and computations.[5]
The research language Opal, which was actively designed up until 1990, also effectively based I/O on a monadic type, but the connection was not realized at the time.[19]
The computer scientist Eugenio Moggi was the first to explicitly link the monad of category theory to functional programming, in a conference paper in 1989,[20]
followed by a more refined journal submission in 1991.
In earlier work, several computer scientists had advanced using category theory to provide semantics for the lambda calculus.
Moggi's key insight was that a real-world program is not just a function from values to other values, but rather a transformation that forms computations on those values.
When formalized in category-theoretic terms, this leads to the conclusion that monads are the structure to represent these computations.[4]
Several others popularized and built on this idea, including Philip Wadler and Simon Peyton Jones, both of whom were involved in the specification of Haskell.
In particular, Haskell used a problematic "lazy stream" model up through v1.2 to reconcile I/O with lazy evaluation, until switching over to a more flexible monadic interface.[21]
The Haskell community would go on to apply monads to many problems in functional programming, and researchers working with Haskell eventually generalized the monad pattern into a wider hierarchy of structures, including applicative functors and arrows.{{citation needed|reason=The early influence of Haskell leaves a clear impression, but is there a comprehensive source for it?|date=October 2018}}
At first, programming with monads was largely confined to Haskell and its derivatives, but as functional programming has influenced other paradigms, many languages have incorporated a monad pattern (in spirit if not in name).
Formulations now exist in Scheme, Perl, Python, Racket, Clojure, Scala, F#, and have also been considered for a new ML standard.{{Citation needed|date=October 2018}}
Analysis
One benefit of the monad pattern is bringing mathematical precision to bear on program logic.
Not only can the monad laws be used to check an instance's validity, but features from related structures (like functors) can be used through subtyping.
Verifying the monad laws
Returning to the Maybe example, its components were declared to make up a monad, but no proof was given that it satisfies the monad laws.
This can be rectified by plugging the specifics of Maybe into one side of the general laws, then algebraically building a chain of equalities to reach the other side:
'''Law 2:''' ma >>= eta(x) ⇔ maif ma is (Just a) then
eta(a) ⇔ Just a
else orNothing ⇔ Nothing
end if '''Law 3:''' '''('''ma >>= f(x)''')''' >>= g(y) ⇔ ma >>= '''('''f(x) >>= g(y)''')''' if (ma >>= f(x)) is (Just b) then if ma is (Just a) theng( ma >>= f(x) ) (f(x) >>= g(y)) a
else elseNothing Nothing
end if end if ⇔ if ma is (Just a) and f(a) is (Just b) then(g ∘ f) a
else if ma is (Just a) and f(a) is Nothing thenNothing
elseNothing
end ifDerivation from functors
Though rarer in computer science, one can use category theory directly, which defines a monad as a functor with two additional natural transformations.
So to begin, a structure requires a higher-order function (or "functional") named map to qualify as a functor:
map φ : (a → b) → (ma → mb)
This is not always a major issue, however, especially when a monad is derived from a pre-existing functor, whereupon the monad inherits {{mvar|map}} automatically.
A monad's first transformation is actually the same {{mvar|unit}} from the Kleisli triple, but following the hierarchy of structures closely, it turns out {{mvar|unit}} characterizes an applicative functor, an intermediate structure between a monad and a basic functor.
In the applicative context, {{mvar|unit}} is sometimes referred to as pure but is still the same function.
What does differ in this construction is the law {{mvar|unit}} must satisfy; as {{mvar|bind}} is not defined, the constraint is given in terms of {{mvar|map}} instead:
(unit ∘ φ) x ↔ ((map φ) ∘ unit) x[22]
The final leap from applicative functor to monad comes with the second transformation, the join function, which "flattens" nested applications of the monad:
join(mma) : M (M T) → M T
As the characteristic function, {{mvar|join}} must also satisfy three variations on the monad laws:{{citation needed|reason=Of all the standard sources, only the Haskell wikibook appears to give the join-based laws; they can, however, be translated from the coherence conditions of category theory|date=October 2018}}
join ∘ (map join) mmma ↔ (join ∘ join) mmma ↔ ma
join ∘ (map unit) ma ↔ (join ∘ unit) ma ↔ ma
join ∘ (map map φ) mma ↔ ((map φ) ∘ join) mma ↔ mb
Regardless of whether a developer defines a direct monad or a Kleisli triple, the underlying structure will be the same, and the forms can be derived from each other easily:
(map φ) ma ↔ ma >>= (unit ∘ φ) x
join(mma) ↔ mma >>= x
ma >>= f(x) ↔ (join ∘ (map f)) ma[23]
Another example: List
The List monad naturally demonstrates how deriving a monad from a simpler functor can come in handy.
In many languages, a list structure comes pre-defined along with some basic features, so a List type constructor and {{mvar|append}} operator (represented with ++ for infix notation) are assumed as already given here.
Embedding a plain value in a list is also trivial in most languages:
From here, applying a function iteratively with a list comprehension may seem like an easy choice for {{mvar|bind}} and converting lists to a full monad.
The difficulty with this approach is that {{mvar|bind}} expects monadic functions, which in this case will output lists themselves;
as more functions are applied, layers of nested lists will accumulate, requiring more than a basic comprehension.
However, a procedure to apply any simple function over the whole list, in other words {{mvar|map}}, is straight-forward:
Now, these two procedures already promote List to an applicative functor.
To fully qualify as a monad, only a correct notion of {{mvar|join}} to flatten repeated structure is needed, but for lists, that just means unwrapping an outer list to append the inner ones that contain values:
join(xlistlist) = join([xlist1, xlist2, ..., xlistn]) = xlist1 ++ xlist2 ++ ... ++ xlistn
The resulting monad is not only a list, but one that automatically resizes and condenses itself as functions are applied.
{{mvar|bind}} can now also be derived with just a formula, then used to feedList values through a pipeline of monadic functions:One application for this monadic list is representing nondeterministic computation.
List can hold results for all execution paths in an algorithm, then condense itself at each step to "forget" which paths led to which results (a sometimes important distinction from deterministic, exhaustive algorithms).
Another benefit is that checks can be embedded in the monad; specific paths can be pruned transparently at their first point of failure, with no need to rewrite functions in the pipeline.[23]
A second situation where List shines is composing multivalued functions.
For instance, the {{mvar|n}}th complex root of a number should yield {{mvar|n}} distinct complex numbers, but if another {{mvar|m}}th root is then taken of those results, the final {{mvar|m•n}} values should be identical to the output of the {{mvar|m•n}}th root.
List completely automates this issue away, condensing the results from each step into a flat, mathematically correct list.[24]Techniques
Monads present opportunities for interesting techniques beyond just organizing program logic. Monads can lay the groundwork for useful syntactic features while their high-level and mathematical nature enable significant abstraction.
Syntax Sugar
Although using {{mvar|bind}} openly often makes sense, many programmers prefer a syntax that mimics imperative statements
(called do-notation in Haskell, perform-notation in OCaml, computation expressions in F#,[25] and for comprehension in Scala).
This is only syntactic sugar that disguises a monadic pipeline as a code block; the compiler will then quietly translate these expressions into underlying functional code.
Translating the add function from the Maybe into Haskell can show this feature in action.
A non-monadic version of add in Haskell looks like this:
add mx my =
case mx of Nothing -> Nothing Just x -> case my of Nothing -> Nothing Just y -> Just (x + y)
In monadic Haskell, return is the standard name for {{mvar|unit}}, plus lambda expressions must be handled explicitly, but even with these technicalities, the Maybe monad makes for a cleaner definition:
add mx my =
mx >>= (\\x -> my >>= (\\y -> return (x + y)))
With do-notation though, this can be distilled even further into a very intuitive sequence:
add mx my = do
x <- mx y <- my return (x + y)
A second example shows how Maybe can be used in an entirely different language: F#.
With computation expressions, a "safe division" function that returns None for an undefined operand or division by zero can be written as:
let readNum () =
let s = Console.ReadLine() let succ,v = Int32.TryParse(s) if (succ) then Some(v) else None
let secure_div =
maybe { let! x = readNum() let! y = readNum() if (y = 0) then None else return (x / y) }At build-time, the compiler will internally "de-sugar" this function into a denser chain of {{mvar|bind}} calls:
maybe.Delay(fun () ->
maybe.Bind(readNum(), fun x -> maybe.Bind(readNum(), fun y -> if (y=0) then None else maybe.Return(x / y))))
For a last example, even the general monad laws themselves can be expressed in do-notation:
do { x <- return v; f x } == do { f v }
do { x <- m; return x } == do { m }
do { y <- do { x <- m; f x }; g y } == do { x <- m; y <- f x; g y }
While convenient, a developer should always remember that this block style is purely syntactic and can be replaced with outwardly monadic (or even non-monadic CPS) expressions.
Using {{mvar|bind}} to express the monadic pipeline can still be clearer in many cases, and some functional programming advocates even argue that since block-style allows novices to carry over habits from imperative programming, it should be avoided by default and only used when obviously superior.[26][2]
General interface
Every monad needs a specific implementation that meets the monad laws, but other aspects like the relation to other structures or standard idioms within a language are shared by all monads.
As a result, a language or library may provide a general Monad interface with function prototypes, subtyping relationships, and other general facts.
Besides providing a head-start to development and guaranteeing a new monad inherits features from a supertype (such as functors), checking a monad's design against the interface adds another layer of quality control.{{citation needed|reason=Not sure of a good general source, but both Gentle Intro to Haskell and Real World Haskell discuss type classes|date=November 2018}}
Operators
Monadic code can often be simplified even further through the judicious use of operators.
The {{mvar|map}} functional can be especially helpful since it works on more than just ad-hoc monadic functions; so long as a monadic function should work analogously to a predefined operator, {{mvar|map}} can be used to instantly "lift" the simpler operator into a monadic one.{{efn|Some languages like Haskell even provide a pseudonym for {{mvar|map}} in other contexts called lift, along with multiple versions for different parameter counts, a detail ignored here.}}
With this technique, the definition of add from the Maybe example could be distilled into:
The process could be taken even one step further by defining add not just for Maybe, but for the whole Monad interface.
By doing this, any new monad that matches the structure interface and implements its own {{mvar|map}} will immediately inherit a lifted version of add too.
The only change to the function needed is generalizing the type signature:
Another monadic operator that is also useful for analysis is monadic composition (represented as infix >=> here), which allows chaining monadic functions in a more mathematical style:
With this operator, the monad laws can be written in terms of functions alone, highlighting the correspondence to associativity and existence of an identity:
(unit >=> g) ↔ g (f >=> unit) ↔ f (f >=> g) >=> h ↔ f >=> (g >=> h)[2]
Variations
At a mathematical level, some monads have particularly nice properties and are uniquely fitted to certain problems.
Additive monads
An additive monad is a monad endowed with an additional closed, associative, binary operator mplus and an identity element under {{mvar|mplus}}, called mzero.
The Maybe monad can be considered additive, with Nothing as {{mvar|mzero}} and a variation on the OR operator as {{mvar|mplus}}.
List is also an additive monad, with the empty list [] acting as {{mvar|mzero}} and the concatenation operator ++ as {{mvar|mplus}}.
Intuitively, {{mvar|mzero}} represents a monadic wrapper with no value from an underlying type, but is also considered a "zero" (rather than a "one") since it acts as an absorber for {{mvar|bind}}, returning {{mvar|mzero}} whenever bound to a monadic function.
This property is two-sided, and {{mvar|bind}} will also return {{mvar|mzero}} when any value is bound to a monadic zero function.
In category-theoretic terms, an additive monad qualifies once as a monoid over monadic functions with {{mvar|bind}} (as all monads do), and again over monadic values via {{mvar|mplus}}.[28]{{efn|Algebraically, the relationship between the two (non-commutative) monoid aspects resembles that of a near-semiring, and some additive monads do qualify as such. However, not all additive monads meet the distributive laws of even a near-semiring.[28]}}
Free monads
Sometimes, the general outline of a monad may be useful, but no simple pattern recommends one monad or another.
This is where a free monad comes in; as a free object in the category of monads, it can represent monadic structure without any specific constraints beyond the monad laws themselves.
Just as a free monoid concatenates elements without evaluation, a free monad allows chaining computations with markers to satisfy the type system, but otherwise imposes no deeper semantics itself.
For example, by working entirely through the Just and Nothing markers, the Maybe monad is in fact a free monad.
The List monad, on the other hand, is not a free monad since it brings extra, specific facts about lists (like {{mvar|append}}) into its definition.
One last example is an abstract free monad, using type markers for {{mvar|unit}} and {{mvar|bind}} and a recursive, linear type constructor:
'''newtype''' Free F(T) = Unit T '''or''' Bind (F, Free F(T)) unit(x) = Unit x mx >>= f = ... '''if''' mx '''is''' Unit x '''then''' ... f(x) '''else''' ... Bind (f,mx) '''end if'''
Free monads, however, are not restricted to a linked-list like in this example, and can be built around other structures like trees.
Using free monads intentionally may seem impractical at first, but their formal nature is particularly well-suited for syntactic problems.
A free monad can be used to track syntax and type while leaving semantics for later, and has found use in parsers and interpreters as a result.[29]
Others have applied them to more dynamic, operational problems too, such as providing iteratees within a language.[30]
Comonads
Besides generating monads with extra properties, for any given monad, one can also define a comonad.
Conceptually, if monads represent computations built up from underlying values, then comonads can be seen as reductions back down to values.
Monadic code, in a sense, cannot be fully "unpacked"; once a value is wrapped within a monad, it remains quarantined there along with any side-effects (a good thing in purely functional programming).
Sometimes though, a problem is more about consuming contextual data, which comonads can model explicitly.
Technically, a comonad is the categorical dual of a monad, which loosely means that it will have the same required components, only with the direction of the type signatures reversed.
Starting from the {{mvar|bind}}-centric monad definition, a comonad consists of:
- A type constructor {{mvar|W}} that marks the higher-order type {{mvar|W T}}
- The dual of {{mvar|unit}}, called counit here, extracts the underlying value from the comonad:
- A reversal of {{mvar|bind}} (also represented with
=>>) that extends a chain of reducing functions:
counit ∘ '''(''' (wa =>> f) → wb ''')''' ↔ f(wa) → b wa =>> counit ↔ wa wa '''(''' (=>> f(wx = wa)) → wb (=>> g(wy = wb)) → wc ''')''' ↔ '''(''' wa (=>> f(wx = wa)) → wb ''')''' (=>> g(wy = wb)) → wcAnalogous to monads, comonads can also be derived from functors using a dual of {{mvar|join}}:
- duplicate takes an already comonadic value and wraps it in another layer of comonadic structure:
While operations like {{mvar|extend}} are reversed, however, a comonad does not reverse functions it acts on, and consequently, comonads are still functors with {{mvar|map}}, not cofunctors.
The alternate definition with {{mvar|duplicate}}, {{mvar|counit}}, and {{mvar|map}} must also respect its own comonad laws:
((map duplicate) ∘ duplicate) wa ↔ (duplicate ∘ duplicate) wa ↔ wwwa ((map counit) ∘ duplicate) wa ↔ (counit ∘ duplicate) wa ↔ wa ((map map φ) ∘ duplicate) wa ↔ (duplicate ∘ (map φ)) wa ↔ wwb
And as with monads, the two forms can be converted automatically:
(map φ) wa ↔ wa =>> (φ ∘ counit) wx duplicate wa ↔ wa =>> wx
A simple example is the Product comonad, which outputs values based on an input value and shared environment data.
In fact, the Product comonad is just the dual of the Writer monad and effectively the same as the Reader monad (both discussed below).
Product and Reader differ only in which function signatures they accept, and how they complement those functions by wrapping or unwrapping values.
A less trivial example is the Stream comonad, which can be used to represent data streams and attach filters to the incoming signals with {{mvar|extend}}.
In fact, while not as popular as monads, researchers have found comonads particularly useful for stream processing and modeling dataflow programming.[31][32]
Due to their strict definitions, however, one cannot simply move objects back and forth between monads and comonads.
As an even higher abstraction, arrows can subsume both structures, but finding more granular ways to combine monadic and comonadic code is an active area of research.[33][34]
More examples
Identity monad
The simplest monad is the Identity monad, which just annotates plain values and functions to satisfy the monad laws:
'''newtype''' Id T = T unit(x) = x (x >>= f) = f(x)
Identity does actually have valid uses though, such as providing a base case for recursive monad transformers.
It can also be used to perform basic variable assignment within an imperative-style block.{{efn|In category theory, the Identity monad can also be viewed as emerging from adjunction of any functor with its inverse.}}{{citation needed|date=October 2018}}
Collections
Any collection with a proper {{mvar|append}} is already a free monoid, but it turns out that List is not the only collection that also has a well-defined {{mvar|join}} and qualifies as a monad.
One can even mutate List into these other monadic collections by simply imposing special properties on {{mvar|append}}:{{efn|Category theory views these collection monads as adjunctions between the free functor and different functors from the category of sets to the category of monoids.}}{{citation needed|date=November 2018}}
| Collection | Monoid properties |
|---|---|
| List | Free |
| Finite multiset | Commutative |
| Finite set | Commutative & idempotent |
| Finite permutations | Non-commutative & idempotent |
I/O monad (Haskell)
As already mentioned, pure code should not have unmanaged side effects, but that does not preclude a program from explicitly describing and managing effects.
This idea is central to Haskell's IO monad, where an object of type IO can be seen as containing the current state of the world outside the program.
When a programmer binds an IO monad to a function, the function makes decisions based on that view of the world (input from users, files, etc.), then yields a monadic value reflecting the new world-state (program output).[35]
For example, Haskell has several functions for acting on the wider file system, including one that checks whether a file exists and another that deletes a file.
Their two type signatures are:
doesFileExist :: FilePath -> IO Bool
removeFile :: FilePath -> IO ()
The first is interested in whether a given file really exists, and as a result, outputs a Boolean value within the IO monad.
The second function, on the other hand, is only concerned with acting on the file system so the IO container it outputs is empty.
IO is not limited just to file I/O though; it even allows for user I/O, and along with imperative syntax sugar, can mimic a typical "Hello, World!" program:
main :: IO ()
main = do
putStrLn "Hello, world!" putStrLn "What is your name, user?" name <- getLine putStrLn ("Nice to meet you, " ++ name ++ "!")Desugared, this translates into the following monadic pipeline (>> in Haskell is just a variant of {{mvar|bind}} for when only monadic effects matter and the underlying result can be discarded):
main :: IO ()
main =
putStrLn "Hello, world!" >> putStrLn "What is your name, user?" >> getLine >>= (\ame -> putStrLn ("Nice to meet you, " ++ name ++ "!"))Writer monad (Javascript)
Another common situation is keeping a log file or otherwise reporting a program's progress.
Sometimes, a programmer may want to log even more specific, technical data for later profiling or debugging.
The Writer monad can handle these tasks by generating auxiliary output that accumulates step-by-step.
To show how the monad pattern isn't restricted to primarily functional languages, this example implements a Writer monad in Javascript.
First, an array (with nested tails) allows constructing the Writer type as a linked list.
The underlying output value will live in position 0 of the array, and position 1 will implicitly hold a chain of auxiliary notes:
Defining {{mvar|unit}} is also very simple:
Only {{mvar|unit}} is needed to define simple functions that output Writer objects with debugging notes:
const squared = x => [x * x, [`${x} was squared.`]];
const halved = x => [x / 2, [`${x} was halved.`]];
A true monad still requires {{mvar|bind}}, but for Writer, this amounts simply to appending a function's output to the monad's linked list:
const bind = (writer, transform) => {
const [value, log] = writer; const [result, updates] = transform(value); return [result, log.concat(updates)];
};
The sample functions can now be chained together using {{mvar|bind}}, but defining a version of monadic composition (called pipelog here) allows applying these functions even more succinctly:
const pipelog = (writer, ...transforms) =>
The final result is a clean separation of concerns between stepping through computations and logging them to audit later:
pipelog(unit(4), squared, halved);
// Resulting writer object = [8, ['4 was squared.', '16 was halved.']]
Environment monad
An environment monad (also called a reader monad and a function monad) allows a computation to depend on values from a shared environment. The monad type constructor maps a type {{mvar|T}} to functions of type {{math|E → T}}, where {{mvar|E}} is the type of the shared environment. The monad functions are:
The following monadic operations are useful:
The {{math|ask}} operation is used to retrieve the current context, while {{math|local}} executes a computation in a modified subcontext. As in a state monad, computations in the environment monad may be invoked by simply providing an environment value and applying it to an instance of the monad.
State monads
A state monad allows a programmer to attach state information of any type to a calculation. Given any value type, the corresponding type in the state monad is a function which accepts a state, then outputs a new state (of type s) along with a return value (of type t). This is similar to an environment monad, except that it also return a new state, and thus allows modeling a mutable environment.
type State s t = s -> (t, s)
Note that this monad, unlike those already seen, takes a type parameter, the type of the state information. The monad operations are defined as follows:
return x = \\s -> (x, s)
-- "bind" modifies m so that it applies f to its result.m >>= f = \\r -> let (x, s) = m r in (f x) s
Useful state operations include:
get = \\s -> (s, s) -- Examine the state at this point in the computation.
put s = \\_ -> ((), s) -- Replace the state.
modify f = \\s -> ((), f s) -- Update the state
Another operation applies a state monad to a given initial state:
runState :: State s a -> s -> (a, s)
runState t s = t s
do-blocks in a state monad are sequences of operations that can examine and update the state data.
Informally, a state monad of state type {{mvar|S}} maps the type of return values {{mvar|T}} into functions of type 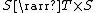 , where {{mvar|S}} is the underlying state. The {{math|return}} and {{math|bind}} function are:
, where {{mvar|S}} is the underlying state. The {{math|return}} and {{math|bind}} function are:
.
From the category theory point of view, a state monad is derived from the adjunction between the product functor and the exponential functor, which exists in any cartesian closed category by definition.
Continuation monad
A continuation monad with return type {{mvar|R}} maps type {{mvar|T}} into functions of type 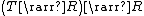 . It is used to model continuation-passing style. The return and bind functions are as follows:
. It is used to model continuation-passing style. The return and bind functions are as follows:
The call-with-current-continuation function is defined as follows:
See also
Alternatives for modeling computations:- Effect systems are a different way to describe side effects as types
- Uniqueness types are a third approach to handling side-effects in functional languages
- Aspect-oriented programming emphasizes separating out ancillary bookkeeping code to improve modularity and simplicity
- Inversion of control is the abstract principle of calling specific functions from an overarching framework
- Type classes are a specific language feature used to implement monads and other structures in Haskell
- The decorator pattern is a more concrete, ad-hoc way to achieve similar benefits in object-oriented programming
- Applicative functors generalize from monads by keeping only {{mvar|unit}} and laws relating it to {{mvar|map}}
- Arrows use additional structure to bring plain functions and monads under a single interface
- Monad transformers act on distinct monads to combine them modularly
Notes
{{notelist}}References
2. ^1 2 3 4 5 6 7 {{cite book | last1 = O'Sullivan | first1 = Bryan | last2 = Goerzen | first2 = John | last3 = Stewart | first3 = Don | title = Real World Haskell | publisher = O'Reilly Media | location = Sebastopol, California | year = 2009 | isbn = 978-0596514983 | chapter = Monads | at = chapter 14 | chapterurl = http://book.realworldhaskell.org/read/monads.html | url = http://book.realworldhaskell.org/}}
3. ^1 {{cite conference | authorlink = Philip Wadler | last = Wadler | first = Philip | title = Comprehending Monads | conference = ACM Conference on LISP and Functional Programming | location = Nice, France | date = June 1990 | citeseerx = 10.1.1.33.5381}}
4. ^1 2 {{cite journal | authorlink = Eugenio Moggi | last = Moggi | first = Eugenio | year = 1991 | title = Notions of computation and monads | journal = Information and Computation | volume = 93 | issue = 1 | pages = 55–92 | url = http://www.disi.unige.it/person/MoggiE/ftp/ic91.pdf | citeseerx = 10.1.1.158.5275}}
5. ^1 2 3 4 {{cite conference | authorlink = Philip Wadler | last = Wadler | first = Philip | title = The essence of functional programming | conference = 19th Annual ACM Symposium on Principles of Programming Languages | location = Albuquerque, New Mexico | date = January 1992 | citeseerx = 10.1.1.38.9516}}
6. ^1 {{cite book | authorlink1 = Paul Hudak | last1 = Hudak | first1 = Paul | last2 = Peterson | first2 = John | last3 = Fasel | first3 = Joseph | title = A Gentle Introduction to Haskell 98 | year = 1999 | chapter = About Monads | at = chapter 9 | chapterurl = https://www.haskell.org/tutorial/monads.html | url = https://www.haskell.org/tutorial/index.html}}
7. ^[https://stackoverflow.com/questions/3322540/how-and-why-does-the-haskell-cont-monad-work C. A. McCann's answer (Jul 23 '10 at 23:39) How and why does the Haskell Cont monad work?]
8. ^{{cite journal | last1 = Spivey | first1 = Mike | year = 1990 | title = A functional theory of exceptions | journal = Science of Computer Programming | volume = 14 | issue = 1 | pages = 25–42 | url = https://www.cs.tufts.edu/comp/150FP/archive/mike-spivey/functional-exns.pdf | doi = 10.1016/0167-6423(90)90056-J}}
9. ^{{cite web | title=Monad laws | url=http://www.haskell.org/haskellwiki/Monad_laws | work=HaskellWiki | publisher=haskell.org | accessdate=14 October 2018}}
10. ^{{cite web | title = What a Monad is not | url = https://wiki.haskell.org/What_a_Monad_is_not | date = 7 October 2018}}
11. ^{{cite conference | last = De Meuter | first = Wolfgang | title = Monads as a theoretical foundation for AOP | conference = International Workshop on Aspect Oriented Programming at ECOOP | date = 1997 | location = Jyväskylä, Finland | url = http://soft.vub.ac.be/Publications/1997/vub-prog-tr-97-10.pdf | citeseerx = 10.1.1.25.8262}}
12. ^{{cite web | url = https://wiki.haskell.org/Monad_(sans_metaphors) | title = Monad (sans metaphors) | website = HaskellWiki | date = 1 November 2009 | accessdate = 24 October 2018}}
13. ^{{cite book | last1 = O'Sullivan | first1 = Bryan | last2 = Goerzen | first2 = John | last3 = Stewart | first3 = Don | title = Real World Haskell | publisher = O'Reilly Media | location = Sebastopol, California | year = 2009 | isbn = 978-0596514983 | chapter = Using Parsec | at = chapter 16 | chapterurl = http://book.realworldhaskell.org/read/using-parsec.html | url = http://book.realworldhaskell.org/}}
14. ^{{cite web | url = https://donsbot.wordpress.com/2007/05/17/roll-your-own-window-manager-tracking-focus-with-a-zipper/ | title = Roll Your Own Window Manager: Tracking Focus with a Zipper | last = Stewart | first = Don | date = 17 May 2007 | website = Control.Monad.Writer | archiveurl = https://web.archive.org/web/20180220194721/https://donsbot.wordpress.com/2007/05/17/roll-your-own-window-manager-tracking-focus-with-a-zipper/ | archivedate = 20 February 2018 | deadurl = no | accessdate = 19 November 2018}}
15. ^{{cite journal | last = Benton | first = Nick | date = 2015 | title = Categorical Monads and Computer Programming | url = https://www.lms.ac.uk/sites/lms.ac.uk/files/2.%20Benton%20-%20Categorical%20Monads%20and%20Computer%20Programming.pdf | journal = London Mathematical Society Impact150 Stories | volume = 1 | accessdate = 19 November 2018}}
16. ^{{cite journal | authorlink = Erik Meijer (computer scientist) | last = Meijer | first = Erik | date = 27 March 2012 | title = Your Mouse is a Database | url = https://queue.acm.org/detail.cfm?id=2169076 | journal = ACM Queue | volume = 10 | issue = 3 | accessdate = 19 November 2018}}
17. ^{{cite journal | authorlink = Kenneth E. Iverson | last = Iverson | first = Kenneth | date = September 1987 | title = A dictionary of APL | url = http://www.jsoftware.com/papers/APLDictionary.htm | journal = APL Quote Quad | volume = 18 | issue = 1 | pages = 5-40 | doi = 10.1145/36983.36984 | issn = 1088-6826 | accessdate = 19 November 2018}}
18. ^{{cite journal | authorlink = Heinrich Kleisli | last = Kleisli | first = Heinrich | date = 1965 | title = Every standard construction is induced by a pair of adjoint functors | url = http://www.ams.org/journals/proc/1965-016-03/S0002-9939-1965-0177024-4/S0002-9939-1965-0177024-4.pdf | journal = Proceedings of the American Mathematical Society | volume = 16 | issue = 3 | pages = 544-546 | doi = 10.1090/S0002-9939-1965-0177024-4 | accessdate = 19 November 2018}}
19. ^{{cite techreport | editor = Peter Pepper | collaboration = The Opal Group | institution = Fachbereich Informatik, Technische Universität Berlin | title = The Programming Language Opal | date = November 1997 | edition = 5th corrected | citeseerx = 10.1.1.40.2748}}
20. ^{{cite conference | authorlink = Eugenio Moggi | last = Moggi | first = Eugenio | title = Computational lambda-calculus and monads | conference = Fourth Annual Symposium on Logic in computer science | location = Pacific Grove, California | date = June 1989 | url = https://www.disi.unige.it/person/MoggiE/ftp/lics89.pdf | citeseerx = 10.1.1.26.2787}}
21. ^{{cite conference | authorlink1 = Simon Peyton Jones | authorlink2 = Philip Wadler | last1 = Peyton Jones | first1 = Simon L. | last2 = Wadler | first2 = Philip | title = Imperative functional programming | date = January 1993 | conference = 20th Annual ACM Symposium on Principles of Programming Languages | location = Charleston, South Carolina | url = https://www.microsoft.com/en-us/research/wp-content/uploads/1993/01/imperative.pdf | citeseerx = 10.1.1.53.2504}}
22. ^{{cite web | title = Applicative functor | url = https://wiki.haskell.org/Applicative_functor | date = 7 May 2018 | website = HaskellWiki | publisher = Haskell.org | archiveurl = https://web.archive.org/web/20181030090822/https://wiki.haskell.org/Applicative_functor | archivedate = 30 October 2018 | deadurl = no | accessdate = 20 November 2018}}
23. ^1 {{cite web | last = Gibbard | first = Cale | title = Monads as containers | url = https://wiki.haskell.org/Monads_as_containers | date = 30 December 2011 | website = HaskellWiki | publisher = Haskell.org | archiveurl = https://web.archive.org/web/20171214235146/https://wiki.haskell.org/Monads_as_containers | archivedate = 14 December 2017 | deadurl = no | accessdate = 20 November 2018}}
24. ^1 {{cite web | last = Piponi | first = Dan | title = You Could Have Invented Monads! (And Maybe You Already Have.) | url = http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html | date = 7 August 2006 | website = A Neighborhood of Infinity | archiveurl = https://web.archive.org/web/20181024193429/http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html | archivedate = 24 October 2018 | deadurl = no | accessdate = 16 October 2018}}
25. ^{{cite web | url = https://blogs.msdn.microsoft.com/dsyme/2007/09/21/some-details-on-f-computation-expressions/ | title = Some Details on F# Computation Expressions | accessdate = 9 October 2018}}
26. ^{{cite web | title = Do notation considered harmful | url = https://wiki.haskell.org/Do_notation_considered_harmful | publisher = HaskellWiki | accessdate = 12 October 2018}}
27. ^{{cite web | last = Giles | first = Brett | title = Lifting | url = https://wiki.haskell.org/Lifting | date = 12 August 2013 | website = HaskellWiki | publisher = Haskell.org | archiveurl = https://web.archive.org/web/20180129230953/https://wiki.haskell.org/Lifting | archivedate = 29 January 2018 | deadurl = no | accessdate = 25 November 2018}}
28. ^1 {{cite conference | last1 = Rivas | first1 = Exequiel | last2 = Jaskelioff | first2 = Mauro | last3 = Schrijvers | first3 = Tom | title = From monoids to near-semirings: the essence of MonadPlus and Alternative | date = July 2015 | conference = 17th International ACM Symposium on Principles and Practice of Declarative Programming | location = Siena, Italy | url = https://usuarios.fceia.unr.edu.ar/~mauro/pubs/FromMonoidstoNearsemirings.pdf | citeseerx = 10.1.1.703.342}}
29. ^{{cite journal | last = Swierstra | first = Wouter | year = 2008 | title = Data types à la carte | journal = Journal of Functional Programming | department = Functional Pearl | volume = 18 | issue = 4 | pages = 423-436 | publisher = Cambridge University Press | issn = 1469-7653 | url = http://www.cs.ru.nl/~W.Swierstra/Publications/DataTypesALaCarte.pdf | citeseerx = 10.1.1.101.4131}}
30. ^{{cite conference | last = Kiselyov | first = Oleg | title = Iteratees | date = May 2012 | conference = International Symposium on Functional and Logic Programming | location = Kobe, Japan | publisher = Springer-Verlag | series = Lecture Notes in Computer Science | volume = 7294 | pages = 166-181 | isbn = 978-3-642-29822-6 | editor-last1 = Schrijvers | editor-first1 = Tom | editor-last2 = Thiemann | editor-first2 = Peter | url = http://okmij.org/ftp/Haskell/Iteratee/describe.pdf | doi = 10.1007/978-3-642-29822-6_15}}
31. ^{{cite conference | last1 = Uustalu | first1 = Tarmo | last2 = Vene | first2 = Varmo | title = The Essence of Dataflow Programming | date = July 2005 | conference = First Summer School, Central European Functional Programming | location = Budapest, Hungary | publisher = Springer-Verlag | series = Lecture Notes in Computer Science | volume = 4164 | pages = 135-167 | isbn = 978-3-540-46845-5 | editor-last = Horváth | editor-first = Zoltán | url = http://www.cs.ioc.ee/~tarmo/papers/cefp05.pdf | citeseerx = 10.1.1.62.2047}}
32. ^{{cite journal | last1 = Uustalu | first1 = Tarmo | last2 = Vene | first2 = Varmo | title = Comonadic Notions of Computation | date = June 2008 | journal = Electronic Notes in Theoretical Computer Science | volume = 203 | issue = 5 | pages = 263-284 | publisher = Elsevier | issn = 1571-0661 | url = https://ac.els-cdn.com/S1571066108003435/1-s2.0-S1571066108003435-main.pdf?_tid=da77d794-4183-481d-b055-009a231d0a66&acdnat=1543174686_71974487fbbc9e6de89e0811c8caeab3 | doi = 10.1016/j.entcs.2008.05.029}}
33. ^{{cite journal | last1 = Power | first1 = John | last2 = Watanabe | first2 = Hiroshi | title = Combining a monad and a comonad | date = May 2002 | journal = Theoretical Computer Science | volume = 280 | issue = 1-2 | pages = 137-162 | publisher = Elsevier | issn = 0304-3975 | url = https://core.ac.uk/download/pdf/82680163.pdf | citeseerx = 10.1.1.35.4130}}
34. ^{{cite conference | last1 = Gaboardi | first1 = Marco | last2 = Katsumata | first2 = Shin-ya | last3 = Orchard | first3 = Dominic | last4 = Breuvart | first4 = Flavien | last5 = Uustalu | first5 = Tarmo | title = Combining Effects and Coeffects via Grading | date = September 2016 | conference = 21st ACM International Conference on Functional Programming | location = Nara, Japan | publisher = Association for Computing Machinery | pages = 476-489 | isbn = 978-1-4503-4219-3 | url = https://www.acsu.buffalo.edu/~gaboardi/publication/GaboardiEtAlicfp16.pdf | doi = 10.1145/2951913.2951939}}
35. ^{{cite conference | authorlink1 = Simon Peyton Jones | authorlink2 = Philip Wadler | last1 = Peyton Jones | first1 = Simon L. | last2 = Wadler | first2 = Philip | title = Imperative functional programming | date = January 1993 | conference = 20th Annual ACM Symposium on Principles of Programming Languages | location = Charleston, South Carolina | url = https://www.microsoft.com/en-us/research/wp-content/uploads/1993/01/imperative.pdf | citeseerx = 10.1.1.53.2504}}
External links
{{Wikibooks|Haskell|Understanding monads}}HaskellWiki references:- "[https://wiki.haskell.org/All_About_Monads All About Monads]" (originally by Jeff Newbern) — A comprehensive discussion of all the common monads and how they work in Haskell; includes the "mechanized assembly line" analogy.
- "[https://wiki.haskell.org/Typeclassopedia Typeclassopedia]" (originally by Brent Yorgey) — A detailed exposition of how the leading typeclasses in Haskell, including monads, interrelate.
- "A Fistful of Monads" (from the online Haskell textbook Learn You a Haskell for Great Good! — A chapter introducing monads from the starting-point of functor and applicative functor typeclasses, including examples.
- "For a Few Monads More" — A second chapter explaining more details and examples, including a
Probabilitymonad for Markov chains. - "Functors, Applicatives, And Monads In Pictures (by Aditya Bhargava) — A quick, humorous, and visual tutorial on monads.
- "UNIX pipes as IO monads" (by Oleg Kiselyov) — A short essay explaining how Unix pipes are effectively monadic.
- [https://github.com/leithaus/XTrace/blob/monadic/src/main/book/content/monadic.pdf Pro Scala: Monadic Design Patterns for the Web] (by Gregory Meredith) — An unpublished, full-length manuscript on how to improve many facets of web development in Scala with monads.
- Anthropometric history
- Anthropometric measurement of the developing fetus
- Anthropomorphic character
- Anthropomorphic character (comics)
- Anthropomorphic characters
- Anthropomorphic characters (comics)
- Anthropomorphism in science
- Anthroponics
- Anthropophagous: The Beast
- Anthropophagus 2
- Anthroposociology
- Anthroposol
- Anthroposophical Society of Chicago
- Anthropos yia oles tis doulies
- Anthurium acaule
- Anthurium crassinervium
- Anthurium pedatoradiatum
- Anthurium schlechtendalii
- Anthurium slechtendahlii
- Anthurium veitchii
- Anthurium warocqueanum
- Anthus brevirostris
- Anthus furcatus brevirostris
- Anthus kakamegae
- Anthus peruvianus



