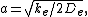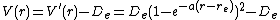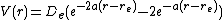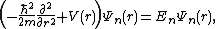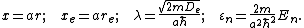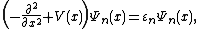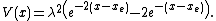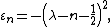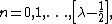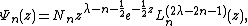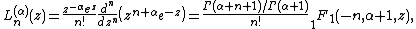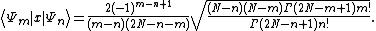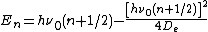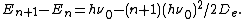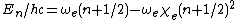请输入您要查询的百科知识：

　

词条 Morse potential
释义

  1. Potential energy function

  2. Vibrational states and energies

  3. Morse/Long-range potential

  4. See also

  5. References

{{Computational physics}}

The Morse potential, named after physicist Philip M. Morse, is a convenient

interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the vibrational structure of the molecule than the QHO (quantum harmonic oscillator) because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone and combination bands. The Morse potential can also be used to model other interactions such as the interaction between an atom and a surface. Due to its simplicity (only three fitting parameters), it is not used in modern spectroscopy. However, its mathematical form inspired the MLR (Morse/Long-range) potential, which is the most popular potential energy function used for fitting spectroscopic data.

Potential energy function

The Morse potential energy function is of the form

Here is the distance between the atoms, is the equilibrium bond distance, 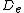is the well depth (defined relative to the dissociated atoms), and controls the 'width' of the potential (the smaller is, the larger the well). The dissociation energy of the bond can be calculated by subtracting the zero point energy from the depth of the well. The force constant (stiffness) of the bond can be found by Taylor expansion of 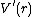around 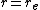to the second derivative of the potential energy function, from which it can be shown that the parameter, , is

where is the force constant at the minimum of the well.

Since the zero of potential energy is arbitrary, the equation for the Morse potential can be rewritten any number of ways by adding or subtracting a constant value. When it is used to model the atom-surface interaction, the energy zero can be redefined so that the Morse potential becomes

which is usually written as

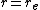where is now the coordinate perpendicular to the surface. This form approaches zero at infinite and equals at its minimum, i.e. . It clearly shows that the Morse potential is the combination of a short-range repulsion term (the former) and a long-range attractive term (the latter), analogous to the Lennard-Jones potential.

Vibrational states and energies

Like the quantum harmonic oscillator, the energies and eigenstates of the Morse potential can be found using operator methods.[1]

One approach involves applying the factorization method to the Hamiltonian.

To write the stationary states on the Morse potential, i.e. solutions 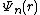and 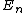of the following Schrödinger equation:

it is convenient to introduce the new variables:

Then, the Schrödinger equation takes the simple form:

Its eigenvalues and eigenstates can be written as:[2]

where

with [x] denoting the largest integer smaller than x.

where

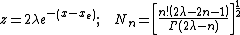and 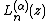is a generalized Laguerre polynomial:

There also exists the following important analytical expression for matrix elements of the coordinate operator (here it is assumed that and )

[3]

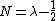The eigenenergies in the initial variables have form:

where is the vibrational quantum number, and has units of frequency, and is mathematically related to the particle mass, , and the Morse constants via

Whereas the energy spacing between vibrational levels in the quantum harmonic oscillator is constant at 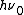, the energy between adjacent levels decreases with increasing in the Morse oscillator. Mathematically, the spacing of Morse levels is

This trend matches the anharmonicity found in real molecules. However, this equation fails above some value of 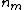where 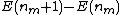is calculated to be zero or negative. Specifically,

integer part.

This failure is due to the finite number of bound levels in the Morse potential, and some maximum 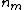that remains bound. For energies above 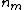, all the possible energy levels are allowed and the equation for 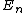is no longer valid.

Below 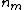, 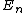is a good approximation for the true vibrational structure in non-rotating diatomic molecules. In fact, the real molecular spectra are generally fit to the form1

in which the constants 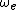and 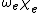can be directly related to the parameters for the Morse potential.

As is clear from dimensional analysis, for historical reasons the last equation uses spectroscopic notation in which 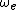represents a wavenumber obeying 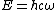, and not an angular frequency given by .

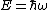Morse/Long-range potential

An important extension of the Morse potential that made the Morse form very useful for modern spectroscopy is the MLR (Morse/Long-range) potential.[4] The MLR potential is used as a standard for representing spectroscopic and/or virial data of diatomic molecules by a potential energy curve. It has been used on N2,[4] Ca2,[5] KLi,[6] MgH,[8][9][7] several electronic states of Li2,[8][9][10][11][12][10] Cs2,[13][14] Sr2,[15] ArXe,[12][16] LiCa,[17] LiNa,[18] Br2,[19] Mg2,[20] HF,[21][22] HCl,[21][22] HBr,[21][22] HI,[21][22] MgD,[23] Be2,[24] BeH,[25] and NaH.[26] More sophisticated versions are used for polyatomic molecules.

See also

  • Morse/Long-range potential
  • Lennard-Jones potential
  • Molecular mechanics

References

  • 1 CRC Handbook of chemistry and physics, Ed David R. Lide, 87th ed, Section 9, SPECTROSCOPIC CONSTANTS OF DIATOMIC MOLECULES pp. 9–82
  • {{cite news

|first1=P. M.
|last1= Morse
|title=Diatomic molecules according to the wave mechanics. II. Vibrational levels
|journal=Phys. Rev.
|year=1929
|volume=34
|pages=57–64
|doi=10.1103/PhysRev.34.57
|bibcode=1929PhRv...34...57M
}}
  • {{cite news

|first1=L. A.
|last1=Girifalco
|first2=G. V.
|last2=Weizer
|title=Application of the Morse Potential Function to cubic metals
|journal= Phys. Rev.
|year=1959
|volume=114
|number=3
|page=687
|doi=10.1103/PhysRev.114.687
|bibcode=1959PhRv..114..687G
}}
  • {{cite news

|first1=Bruce W.
|last1=Shore
|title=Comparison of matrix methods applied to the radial Schrödinger eigenvalue equation: The Morse potential
|year=1973
|doi=10.1063/1.1680025
|journal= J. Chem. Phys.
|volume=59
|number=12
|page=6450
|bibcode=1973JChPh..59.6450S
}}
  • {{cite news

|first1=Robert W.
|last1=Keyes
|title=Bonding and antibonding potentials in group-IV semiconductors
|journal=Phys. Rev. Lett.
|year=1975
|volume=34
|number=21
|pages=1334–1337
|doi=10.1103/PhysRevLett.34.1334
|bibcode=1975PhRvL..34.1334K
}}
  • {{cite news

|first1=R. C.
|last1=Lincoln
|first2=K. M.
|last2=Kilowad
|first3=P. B.
|last3=Ghate
|title=Morse-potential evaluation of second- and third-order elastic constants of some cubic metals
|year=1967
|pages=463–466
|journal=Phys. Rev.
|volume=157
|number=3
|doi=10.1103/PhysRev.157.463
|bibcode=1967PhRv..157..463L
}}
  • {{cite news

|first1=Shi-Hai
|last1=Dong
|first2=R.
|last2=Lemus
|first3=A.
|last3=Frank
|title=Ladder operators for the Morse potential
|journal=Int. J. Quantum Chem.
|year=2001
|doi=10.1002/qua.10038
|volume=86
|number=5
|pages=433–439
}}
  • {{ cite news

|first1=Yaoqi
|last1=Zhou
|first2=Martin
|last2=Karplus
|first3=Keith D.
|last3=Ball
|first4=R. Stephen
|last4=Bery
|title=The distance fluctuation criterion for melting: Comparison of square-well and Morse Potential models for clusters and homopolymers
|journal=J. Chem. Phys.
|volume=116
|number=5
|pages=2323–2329
|year=2002
|doi=10.1063/1.1426419
}}
  • I.G. Kaplan, in Handbook of Molecular Physics and Quantum Chemistry, Wiley, 2003, p207.
1. ^F. Cooper, A. Khare, U. Sukhatme, Supersymmetry in Quantum Mechanics, World Scientific, 2001, Table 4.1
2. ^{{cite journal | last1 = Dahl | first1 = J.P. | last2 = Springborg | first2 = M. | title = The Morse Oscillator in Position Space, Momentum Space, and Phase Space | url = http://orbit.dtu.dk/files/3620619/Dahl.pdf| journal = J. Chem. Phys. | volume = 88 | issue = 7 | page = 4535| year = 1988 | doi=10.1063/1.453761|bibcode = 1988JChPh..88.4535D }}
3. ^E. F. Lima and J. E. M. Hornos, "Matrix Elements for the Morse Potential Under an External Field", J. Phys. B: At. Mol. Opt. Phys. 38, pp. 815-825 (2005)
4. ^{{cite journal|last=Le Roy|first=R. J.|author2=Y. Huang |author3=C. Jary |title=An accurate analytic potential function for ground-state N2 from a direct-potential-fit analysis of spectroscopic data|journal=Journal of Chemical Physics|year=2006|volume=125|issue=16|page=164310|doi=10.1063/1.2354502|pmid=17092076|bibcode=2006JChPh.125p4310L}}
5. ^{{cite journal|last=Le Roy|first=Robert J.|author2=R. D. E. Henderson|title=A new potential function form incorporating extended long-range behaviour: application to ground-state Ca2|journal=Molecular Physics|year=2007|volume=105|issue=5–7|pages=663–677|doi=10.1080/00268970701241656|bibcode=2007MolPh.105..663L}}
6. ^{{cite journal|last=Salami|first=H.|author2=A. J. Ross |author3=P. Crozet |author4=W. Jastrzebski |author5=P. Kowalczyk |author6=R. J. Le Roy |title=A full analytic potential energy curve for the a3Σ+ state of KLi from a limited vibrational data set|journal=Journal of Chemical Physics|year=2007|volume=126|issue=19|page=194313|doi=10.1063/1.2734973|pmid=17523810|bibcode=2007JChPh.126s4313S}}
7. ^{{cite journal|last=Shayesteh|first=A.|author2=R. D. E. Henderson |author3=R. J. Le Roy |author4=P. F. Bernath |title=Ground State Potential Energy Curve and Dissociation Energy of MgH|journal=The Journal of Physical Chemistry A|year=2007|volume=111|issue=49|pages=12495–12505|doi=10.1021/jp075704a|bibcode=2007JPCA..11112495S |pmid=18020428|citeseerx=10.1.1.584.8808}}
8. ^1 {{cite journal|last=Le Roy|first=Robert J.|author2=N. S. Dattani |author3=J. A. Coxon |author4=A. J. Ross |author5=Patrick Crozet |author6=C. Linton |title=Accurate analytic potentials for Li2(X) and Li2(A) from 2 to 90 Angstroms, and the radiative lifetime of Li(2p)|journal=Journal of Chemical Physics|date=25 November 2009|volume=131|issue=20|page=204309|doi=10.1063/1.3264688|pmid=19947682|bibcode=2009JChPh.131t4309L}}
9. ^{{cite journal|last=Dattani|first=N. S.|author2=R. J. Le Roy|title=A DPF data analysis yields accurate analytic potentials for Li2(a) and Li2(c) that incorporate 3-state mixing near the c-state asymptote|journal=Journal of Molecular Spectroscopy (Special Issue)|date=8 May 2013|volume=268|issue=1–2|pages=199–210|doi=10.1016/j.jms.2011.03.030|url=http://www.sciencedirect.com/science/article/pii/S0022285211000853#|bibcode= 2011JMoSp.268..199.|arxiv = 1101.1361 }}
10. ^1 W. Gunton, M. Semczuk, N. S. Dattani, K. W. Madison, High resolution photoassociation spectroscopy of the 6Li2 A-state, https://arxiv.org/abs/1309.5870
11. ^{{cite news|first1=M.|last1= Semczuk|first2=X.|last2= Li|first3=W.|last3= Gunton|first4=M.|last4= Haw|first5=N. S.|last5= Dattani|first6=J.|last6= Witz|first7=A. K.|last7= Mills|first8=D. J.|last8= Jones|first9=K. W.|last9= Madison |title=High-resolution photoassociation spectroscopy of the 6Li2 c-state|journal=Phys. Rev. A|year=2013|volume=87|pages=052505|doi=10.1103/PhysRevA.87.052505|url=http://pra.aps.org/abstract/PRA/v87/i5/e052505|arxiv=1309.6662|bibcode=2013PhRvA..87e2505S}}
12. ^1 2 {{cite journal|last=Le Roy|first=R. J.|author2=C. C. Haugen |author3=J. Tao |author4=H. Li |title=Long-range damping functions improve the short-range behaviour of 'MLR' potential energy functions|journal=Molecular Physics|date=February 2011|volume=109|issue=3|pages=435–446|url=http://scienide2.uwaterloo.ca/~rleroy/Pubn/11MolP_damping.pdf|doi=10.1080/00268976.2010.527304|bibcode = 2011MolPh.109..435L }}
13. ^{{cite journal|last=Xie|first=F.|author2=L. Li |author3=D. Li |author4=V. B. Sovkov |author5=K. V. Minaev |author6=V. S. Ivanov |author7=A. M. Lyyra |author8=S. Magnier |title=Joint analysis of the Cs2 a-state and 1 g (33Π1g ) states|journal=Journal of Chemical Physics|year=2011|volume=135|issue=2|page=02403|doi=10.1063/1.3606397|pmid=21766938|bibcode=2011JChPh.135b4303X}}
14. ^{{cite journal|last=Coxon|first=J. A.|author2=P. G. Hajigeorgiou|title=The ground X 1Σ+g electronic state of the cesium dimer: Application of a direct potential fitting procedure|journal=Journal of Chemical Physics|year=2010|volume=132|issue=9|page=094105|doi=10.1063/1.3319739|bibcode=2010JChPh.132i4105C}}
15. ^{{cite journal|last=Stein|first=A.|author2=H. Knockel |author3=E. Tiemann |title=The 1S+1S asymptote of Sr2 studied by Fourier-transform spectroscopy|journal=The European Physical Journal D|date=April 2010|volume=57|issue=2|pages=171–177|doi=10.1140/epjd/e2010-00058-y|bibcode=2010EPJD...57..171S|arxiv = 1001.2741 }}
16. ^{{cite journal|last=Piticco|first=Lorena|author2=F. Merkt |author3=A. A. Cholewinski |author4=F. R. W. McCourt |author5=R. J. Le Roy |title=Rovibrational structure and potential energy function of the ground electronic state of ArXe|journal=Journal of Molecular Spectroscopy|date=December 2010|volume=264|issue=2|pages=83–93|url=http://www.sciencedirect.com/science/article/pii/S002228521000189X|doi=10.1016/j.jms.2010.08.007|bibcode=2010JMoSp.264...83P}}
17. ^{{cite journal|last=Ivanova|first=Milena|author2=A. Stein |author3=A. Pashov |author4=A. V. Stolyarov |author5=H. Knockel |author6=E. Tiemann |title=The X2Σ+ state of LiCa studied by Fourier-transform spectroscopy|journal=Journal of Chemical Physics|year=2011|volume=135|issue=17|page=174303|doi=10.1063/1.3652755|bibcode=2011JChPh.135q4303I}}
18. ^{{cite journal|last=Steinke|first=M.|author2=H. Knockel |author3=E. Tiemann |title=X-state of LiNa studied by Fourier-transform spectroscopy|journal=Physical Review A|date=27 April 2012|volume=85|issue=4|page=042720|doi=10.1103/PhysRevA.85.042720|url=http://pra.aps.org/abstract/PRA/v85/i4/e042720|bibcode=2012PhRvA..85d2720S}}
19. ^{{cite journal|last=Yukiya|first=T.|author2=N. Nishimiya |author3=Y. Samejima |author4=K. Yamaguchi |author5=M. Suzuki |author6=C. D. Boonec |author7=I. Ozier |author8=R. J. Le Roy |title=Direct-potential-fit analysis for the system of Br2|journal=Journal of Molecular Spectroscopy|date=January 2013|volume=283|pages=32–43|url=http://www.sciencedirect.com/science/article/pii/S0022285212002354|doi=10.1016/j.jms.2012.12.006|bibcode=2013JMoSp.283...32Y}}
20. ^{{cite journal|last=Knockel|first=H.|author2=S. Ruhmann |author3=E. Tiemann |title=The X-state of Mg2 studied by Fourier-transform spectroscopy|journal=Journal of Chemical Physics|year=2013|volume=138|issue=9|page=094303|doi=10.1063/1.4792725|pmid=23485290|bibcode=2013JChPh.138i4303K}}
21. ^1 2 3 {{cite journal|last=Li|first=Gang|author2=I. E. Gordon |author3=P. G. Hajigeorgiou |author4=J. A. Coxon |author5=L. S. Rothman |title=Reference spectroscopic data for hydrogen halides, Part II:The line lists|journal=Journal of Quantitative Spectroscopy & Radiative Transfer|date=July 2013|volume=130|pages=284–295|url=http://www.sciencedirect.com/science/article/pii/S0022407313003026|doi=10.1016/j.jqsrt.2013.07.019|bibcode=2013JQSRT.130..284L}}
22. ^1 2 3 {{cite journal | url = http://www.sciencedirect.com/science/article/pii/S0022407314003781 | doi=10.1016/j.jqsrt.2014.08.028 | volume=151 | title=Improved direct potential fit analyses for the ground electronic states of the hydrogen halides: HF/DF/TF, HCl/DCl/TCl, HBr/DBr/TBr and HI/DI/TI | journal=Journal of Quantitative Spectroscopy and Radiative Transfer | pages=133–154|bibcode = 2015JQSRT.151..133C | last1=Coxon | first1=John A. | last2=Hajigeorgiou | first2=Photos G. | year=2015 }}
23. ^1 {{cite journal|last=Henderson|first=R. D. E.|author2=A. Shayesteh |author3=J. Tao |author4=C. Haugen |author5=P. F. Bernath |author6=R. J. Le Roy |title=Accurate Analytic Potential and Born–Oppenheimer Breakdown Functions for MgH and MgD from a Direct-Potential-Fit Data Analysis|journal=The Journal of Physical Chemistry A|volume=117|issue=50|pages=131028105904004|date=4 October 2013|doi=10.1021/jp406680r|bibcode = 2013JPCA..11713373H }}
24. ^{{Cite journal | doi=10.1063/1.4864355|title = Direct-potential-fit analyses yield improved empirical potentials for the ground XΣg+1 state of Be2| journal=The Journal of Chemical Physics| volume=140| issue=6| pages=064315|year = 2014|last1 = Meshkov|first1 = Vladimir V.| last2=Stolyarov| first2=Andrey V.| last3=Heaven| first3=Michael C.| last4=Haugen| first4=Carl| last5=Leroy| first5=Robert J.}}
25. ^{{cite journal | url = http://www.sciencedirect.com/science/article/pii/S0022285214001945 | doi=10.1016/j.jms.2014.09.005 | volume=311 | title=Beryllium monohydride (BeH): Where we are now, after 86 years of spectroscopy | journal=Journal of Molecular Spectroscopy | pages=76–83|arxiv = 1408.3301 |bibcode = 2015JMoSp.311...76D | last1=Dattani | first1=Nikesh S. | last2=Le Roy | first2=Robert J. | year=2015 }}
26. ^{{Cite journal | doi=10.1063/1.4906086|title = Dissociation energies and potential energy functions for the ground X 1Σ+ and "avoided-crossing" A 1Σ+ states of NaH| journal=The Journal of Chemical Physics| volume=142| issue=4| pages=044305|year = 2015|last1 = Walji|first1 = Sadru-Dean| last2=Sentjens| first2=Katherine M.| last3=Le Roy| first3=Robert J.}}
{{DEFAULTSORT:Morse Potential}}

4 : Chemical bonding|Quantum chemistry|Quantum models|Potentials
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 4:33:17