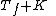“Toeplitz algebra”的意思、由来-开放百科全书

词条

Toeplitz algebra

释义

References

In operator algebras, the Toeplitz algebra is the C*-algebra generated by the unilateral shift on the Hilbert space l²(N).^[1] Taking l²(N) to be the Hardy space H², the Toeplitz algebra consists of elements of the form

where T_f is a Toeplitz operator with continuous symbol and K is a compact operator.

Toeplitz operators with continuous symbols commute modulo the compact operators. So the Toeplitz algebra can be viewed as the C*-algebra extension of continuous functions on the circle by the compact operators. This extension is called the Toeplitz extension.

By Atkinson's theorem, an element of the Toeplitz algebra T_f + K is a Fredholm operator if and only if the symbol f of T_f is invertible. In that case, the Fredholm index of T_f + K is precisely the winding number of f, the equivalence class of f in the fundamental group of the circle. This is a special case of the Atiyah-Singer index theorem.

Wold decomposition characterizes proper isometries acting on a Hilbert space. From this, together with properties of Toeplitz operators, one can conclude that the Toeplitz algebra is the universal C*-algebra generated by a proper isometry; this is Coburn's theorem.

References

1. ^{{citation|title=A Short Course in Spectral Theory|volume=209|series=Graduate Texts in Mathematics|first=Arveson|last=William|publisher=Springer|isbn=0387953000}}

1 : C*-algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。