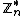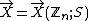“Toida's conjecture”的意思、由来-开放百科全书

词条

Toida's conjecture

释义

Proofs
Notes

In combinatorial mathematics, Toida's conjecture, due to Shunichi Toida in 1977,^[1] is a refinement of the disproven Ádám's conjecture in 1967. Toida's conjecture states formally:

S is a subset of

and

then 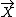is a CI-digraph.

Proofs

The conjecture was proven in the special case where n is a prime power by Klin and Poschel in 1978,^[2] and by Golfand, Najmark, and Poschel in 1984.^[3]

The conjecture was then fully proven by Muzychuk, Klin, and Poschel in 2001 by using Schur algebra,^[4] and simultaneously by Dobson and Morris in 2002 by using the classification of finite simple groups.^[5]

Notes

1. ^*S. Toida: "A note on Adam's conjecture", Journal of Combinatorial Theory (B), pp. 239–246, October–December 1977
2. ^*Klin, M.H. and R. Poschel: The Konig problem, the isomorphism problem for cyclic graphs and the method of Schur rings, Algebraic methods in graph theory, Vol. I, II., Szeged, 1978, pp. 405–434.
3. ^*Golfand, J.J., N.L. Najmark and R. Poschel: The structure of S-rings over Z2m , preprint (1984).
4. ^Klin, M.H., M. Muzychuk and R. Poschel: The isomorphism problem for circulant graphs via Schur ring theory, Codes and Association Schemes, American Math. Society, 2001.
5. ^*E. Dobson, J. Morris: TOIDA’S CONJECTURE IS TRUE, PhD Thesis, 2002.

2 : Combinatorics|Conjectures that have been proved

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。