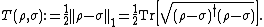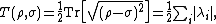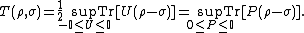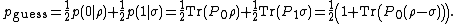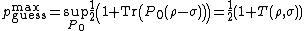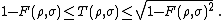“Trace distance”的意思、由来-开放百科全书

词条

Trace distance

释义

Definition
Physical interpretation
Properties
Relationship to other distance measures Fidelity Total variation distance
References

In quantum mechanics, and especially quantum information and the study of open quantum systems, the trace distance T is a metric on the space of density matrices and gives a measure of the distinguishability between two states. It is the quantum generalization of the Kolmogorov distance for classical probability distributions.

Definition

The trace distance is just half of the trace norm of the difference of the matrices:

(The trace norm is the Schatten norm for p=1.) The purpose of the factor of two is to restrict the trace distance between two normalized density matrices to the range [0, 1] and to simplify formulas in which the trace distance appears.

Since density matrices are Hermitian,

where the are eigenvalues of the Hermitian, but not necessarily positive, matrix .

Physical interpretation

By using the Hölder duality for Schatten norms, the trace distance can be written in variational form as ^[1]

As for its classical counterpart, the trace distance can be related to the maximum probability of distinguishing between two quantum states:

For example, suppose Alice prepares a system in either the state or , each with probability and sends it to Bob who has to discriminate between the two states using a binary measurement.

Let Bob assign the measurement outcome and a POVM element such as the outcome and a POVM element 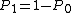to identify the state or , respectively. His expected probability of correctly identifying the incoming state is then given by

Therefore, when applying an optimal measurement, Bob has the maximal probability

of correctly identifying in which state Alice prepared the system.^[2].

Properties

The trace distance has the following properties^[1]

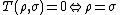
It is a metric on the space of density matrices, i.e. it is non-negative, symmetric, and satisfies the triangle inequality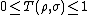, and
and 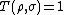if and only if and have orthogonal supports
It is preserved under unitary transformations:
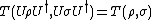
It is contractive under trace-preserving CP maps, i.e. if is a CPT map, then
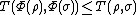
It is convex in each of its inputs. E.g.

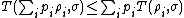
For qubits, the trace distance is equal to half the Euclidean distance in the Bloch representation.

Relationship to other distance measures

Fidelity

The fidelity of two quantum states 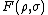is related to the trace distance 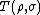by the inequalities

The upper bound inequality becomes an equality when and are pure states.

Total variation distance

The trace distance is a generalization of the total variation distance, and for two commuting density matrices, has the same value as the total variation distance of the two corresponding probability distributions.

References

1. ^¹{{Cite book|last1=Nielsen|first=Michael A.|authorlink1=Michael Nielsen|last2=Chuang|first2=Isaac L.|authorlink2=Isaac Chuang|title=Quantum Computation and Quantum Information|publisher=Cambridge University Press|location=Cambridge|year=2010|edition=2nd|oclc=844974180|isbn=978-1-107-00217-3|chapter=9. Distance measures for quantum information}}
2. ^S. M. Barnett, "Quantum Information", Oxford University Press, 2009, Chapter 4

2 : Quantum information science|Quantum mechanics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。