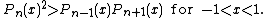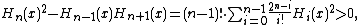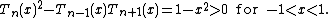- See also
- References
In mathematics, Turán's inequalities are some inequalities for Legendre polynomials found by {{harvs|txt=yes|first=Paul |last=Turán|authorlink=Pál Turán|year=1950}} (and first published by {{harvtxt|Szegö|1948}}). There are many generalizations to other polynomials, often called Turán's inequalities, given by {{harvs|mr=0040487
|last=Beckenbach|first= E. F.|last2= Seidel|first2= W.|last3= Szász|first3= Otto
|title=Recurrent determinants of Legendre and of ultraspherical polynomials
|journal=Duke Math. J.|volume= 18|year=1951|pages= 1–10}} and other authors.
If {{math|Pn}} is the {{mvar|n}}th Legendre polynomial, Turán's inequalities state that
For Hn, the nth Hermite polynomial, Turán's inequalities are
whilst for Chebyshev polynomials they are
See also
- Askey–Gasper inequality
- Sturm Chain
References
- {{citation|mr=0040487
|last=Beckenbach|first= E. F.|last2= Seidel|first2= W.|last3= Szász|first3= Otto
|title=Recurrent determinants of Legendre and of ultraspherical polynomials
|journal=Duke Math. J.|volume= 18|year=1951|pages= 1–10|doi=10.1215/S0012-7094-51-01801-7}}
- {{citation|mr=0023954
|last=Szegö|first= G.
|title=On an inequality of P. Turán concerning Legendre polynomials
|journal=Bull. Amer. Math. Soc. |year=1948|pages= 401–405
|doi=10.1090/S0002-9904-1948-09017-6|volume=54|issue=4 }}
- {{citation|mr=0041284
|last=Turán|first= Paul
|title=On the zeros of the polynomials of Legendre
|journal=Časopis Pěst. Mat. Fys. |volume=75|year=1950|pages= 113–122}}{{DEFAULTSORT:Turan's inequalities}}{{mathanalysis-stub}}
2 : Orthogonal polynomials|Inequalities