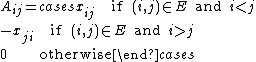“Tutte matrix”的意思、由来-开放百科全书

词条

Tutte matrix

释义

References

In graph theory, the Tutte matrix A of a graph G = (V, E) is a matrix used to determine the existence of a perfect matching: that is, a set of edges which is incident with each vertex exactly once.

If the set of vertices is then the Tutte matrix is an n × n matrix A with entries

where the x_ij are indeterminates. The determinant of this skew-symmetric matrix is then a polynomial (in the variables x_ij, i < j ): this coincides with the square of the pfaffian of the matrix A and is non-zero (as a polynomial) if and only if a perfect matching exists. (This polynomial is not the Tutte polynomial of G.)

The Tutte matrix is named after W. T. Tutte, and is a generalisation of the Edmonds matrix for a balanced bipartite graph.

References

{{cite book|author=R. Motwani, P. Raghavan |title=Randomized Algorithms|publisher=Cambridge University Press|year=1995|page=167}}
{{cite book|author=Allen B. Tucker|title=Computer Science Handbook|publisher=CRC Press|date=2004|isbn=1-58488-360-X|page=12.19}}
{{cite journal|url= http://jlms.oxfordjournals.org/cgi/reprint/s1-22/2/107.pdf|title= The factorization of linear graphs

|accessdate= 2008-06-15|author= W.T. Tutte|authorlink=W. T. Tutte|date=April 1947|volume=22|journal=J. London Math. Soc.|pages=107–111|doi=10.1112/jlms/s1-22.2.107|issue= 2}}{{Matrix classes}}{{combin-stub}}

3 : Algebraic graph theory|Matching|Matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。