“Tversky index”的意思、由来-开放百科全书

词条

Tversky index

释义

Notes

The Tversky index, named after Amos Tversky,^[1] is an asymmetric similarity measure on sets that compares a variant to a prototype. The Tversky index can be seen as a generalization of Dice's coefficient and Tanimoto coefficient (aka Jaccard index).

For sets X and Y the Tversky index is a number between 0 and 1 given by

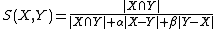Here, denotes the relative complement of Y in X.

Further, 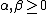are parameters of the Tversky index. Setting produces the Tanimoto coefficient; setting 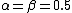produces Dice's coefficient.

If we consider X to be the prototype and Y to be the variant, then corresponds to the weight of the prototype and 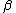corresponds to the weight of the variant. Tversky measures with 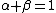are of special interest.^[2]

Because of the inherent asymmetry, the Tversky index does not meet the criteria for a similarity metric. However, if symmetry is needed a variant of the original formulation has been proposed using max and min functions ^[3]

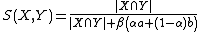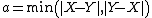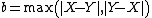This formulation also re-arranges parameters and 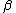. Thus, controls the balance between 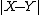and 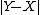in the denominator. Similarly, 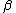controls the effect of the symmetric difference 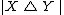versus 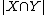in the denominator.

Notes

1. ^{{cite journal |last=Tversky |first=Amos |title=Features of Similarity |journal=Psychological Review |volume=84 |number=4 |year=1977 |pages=327–352 |url=http://www.cogsci.ucsd.edu/~coulson/203/tversky-features.pdf |doi=10.1037/0033-295x.84.4.327}}
2. ^http://www.daylight.com/dayhtml/doc/theory/theory.finger.html
3. ^Jimenez, S., Becerra, C., Gelbukh, A. SOFTCARDINALITY-CORE: Improving Text Overlap with Distributional Measures for Semantic Textual Similarity. Second Joint Conference on Lexical and Computational Semantics (*SEM), Volume 1: Proceedings of the Main Conference and the Shared Task: Semantic Textual Similarity, p.194-201, June 7–8, 2013, Atlanta, Georgia, USA.

5 : Index numbers|String similarity measures|Measure theory|Similarity and distance measures|Asymmetry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。