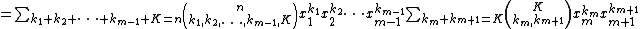“Multinomial theorem”的意思、由来-开放百科全书

词条

Multinomial theorem

释义

Theorem
Example Alternate expression Proof
Multinomial coefficients
Sum of all multinomial coefficients Number of multinomial coefficients Valuation of multinomial coefficients
Interpretations
Ways to put objects into bins Number of ways to select according to a distribution Number of unique permutations of words Generalized Pascal's triangle
See also
References

In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.

Theorem

For any positive integer m and any nonnegative integer n, the multinomial formula tells us how a sum with m terms expands when raised to an arbitrary power n:

where

is a multinomial coefficient. The sum is taken over all combinations of nonnegative integer indices k₁ through k_m such that the sum of all k_i is n. That is, for each term in the expansion, the exponents of the x_i must add up to n. Also, as with the binomial theorem, quantities of the form x⁰ that appear are taken to equal 1 (even when x equals zero).

In the case m = 2, this statement reduces to that of the binomial theorem.

Example

The third power of the trinomial a + b + c is given by

This can be computed by hand using the distributive property of multiplication over addition, but it can also be done (perhaps more easily) with the multinomial theorem, which gives us a simple formula for any coefficient we might want. It is possible to "read off" the multinomial coefficients from the terms by using the multinomial coefficient formula. For example:

has the coefficient

Alternate expression

The statement of the theorem can be written concisely using multiindices:

where

and

Proof

This proof of the multinomial theorem uses the binomial theorem and induction on m.

First, for m = 1, both sides equal x₁ⁿ since there is only one term k₁ = n in the sum. For the induction step, suppose the multinomial theorem holds for m. Then

by the induction hypothesis. Applying the binomial theorem to the last factor,

which completes the induction. The last step follows because

as can easily be seen by writing the three coefficients using factorials as follows:

Multinomial coefficients

The numbers

appearing in the theorem are the multinomial coefficients. They can be expressed in numerous ways, including as a product of binomial coefficients or of factorials:

Sum of all multinomial coefficients

The substitution of x_i = 1 for all i into the multinomial theorem

gives immediately that

Number of multinomial coefficients

The number of terms in a multinomial sum, #_n,m, is equal to the number of monomials of degree n on the variables x₁, …, x_m:

The count can be performed easily using the method of stars and bars.

Valuation of multinomial coefficients

The largest power of a prime that divides a multinomial coefficient may be computed using a generalization of Kummer's theorem.

Interpretations

Ways to put objects into bins

The multinomial coefficients have a direct combinatorial interpretation, as the number of ways of depositing n distinct objects into m distinct bins, with k₁ objects in the first bin, k₂ objects in the second bin, and so on.^[1]

Number of ways to select according to a distribution

In statistical mechanics and combinatorics if one has a number distribution of labels then the multinomial coefficients naturally arise from the binomial coefficients. Given a number distribution {n_i} on a set of N total items, n_i represents the number of items to be given the label i. (In statistical mechanics i is the label of the energy state.)

The number of arrangements is found by

Choosing n₁ of the total N to be labeled 1. This can be done ways.
From the remaining N − n₁ items choose n₂ to label 2. This can be done ways.
From the remaining N − n₁ − n₂ items choose n₃ to label 3. Again, this can be done ways.

Multiplying the number of choices at each step results in:

Upon cancellation, we arrive at the formula given in the introduction.

Number of unique permutations of words

The multinomial coefficient is also the number of distinct ways to permute a multiset of n elements, and k_i are the multiplicities of each of the distinct elements. For example, the number of distinct permutations of the letters of the word MISSISSIPPI, which has 1 M, 4 Is, 4 Ss, and 2 Ps is

(This is just like saying that there are 11! ways to permute the letters—the common interpretation of factorial as the number of unique permutations. However, we created duplicate permutations, because some letters are the same, and must divide to correct our answer.)

Generalized Pascal's triangle

One can use the multinomial theorem to generalize Pascal's triangle or Pascal's pyramid to Pascal's simplex. This provides a quick way to generate a lookup table for multinomial coefficients.

References

1. ^{{cite web |url=http://dlmf.nist.gov/ |title=NIST Digital Library of Mathematical Functions |author=National Institute of Standards and Technology |date=May 11, 2010 |at=Section 26.4 |accessdate=August 30, 2010}}

3 : Factorial and binomial topics|Articles containing proofs|Theorems in algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。