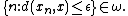请输入您要查询的百科知识：

　

词条 Ultralimit
释义

  1. Ultrafilters

  2. Limit of a sequence of points with respect to an ultrafilter

  3. Ultralimit of metric spaces with specified base-points

  4. On basepoints in the case of uniformly bounded spaces

  5. Basic properties of ultralimits

  6. Asymptotic cones

  7. Examples

  8. Footnotes

  9. Basic References

  10. See also

For the direct limit of a sequence of ultrapowers, see Ultraproduct.

In mathematics, an ultralimit is a geometric construction that assigns to a sequence of metric spaces Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter to avoid the process of repeatedly passing to subsequences to ensure convergence. An ultralimit is a generalization of the notion of Gromov–Hausdorff convergence of metric spaces.

Ultrafilters

Recall that an ultrafilter ω on the set of natural numbers {{math|ℕ}} is a set of nonempty subsets of {{math|ℕ}} (whose inclusion function can thought of as a measure) which is closed under finite intersection, upwards-closed, and which, given any subset X of {{math|ℕ}}, contains either X or {{math|ℕ∖ X}}. An ultrafilter ω on {{math|ℕ}} is non-principal if it contains no finite set.

Limit of a sequence of points with respect to an ultrafilter

Let ω be a non-principal ultrafilter on .

If 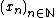is a sequence of points in a metric space (X,d) and x∈ X, the point x is called the ω -limit of xn, denoted 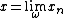, if for every 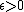we have:

It is not hard to see the following:

  • If an ω -limit of a sequence of points exists, it is unique.
  • If 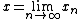in the standard sense, 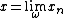. (For this property to hold it is crucial that the ultrafilter be non-principal.)

An important basic fact[1] states that, if (X,d) is compact and ω is a non-principal ultrafilter on , the ω-limit of any sequence of points in X exists (and is necessarily unique).

In particular, any bounded sequence of real numbers has a well-defined ω-limit in (as closed intervals are compact).

Ultralimit of metric spaces with specified base-points

Let ω be a non-principal ultrafilter on . Let (Xn,dn) be a sequence of metric spaces with specified base-points pn∈Xn.

Let us say that a sequence 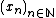, where xn∈Xn, is admissible, if the sequence of real numbers (dn(xn,pn))n is bounded, that is, if there exists a positive real number C such that .

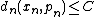Let us denote the set of all admissible sequences by .

It is easy to see from the triangle inequality that for any two admissible sequences 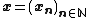and 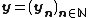the sequence (dn(xn,yn))n is bounded and hence there exists an ω-limit 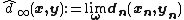. Let us define a relation on the set of all admissible sequences as follows. For 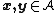we have 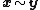whenever 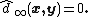It is easy to show that is an equivalence relation on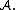

The ultralimit with respect to ω of the sequence (Xn,dn, pn) is a metric space 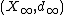defined as follows.[1]

As a set, we have .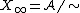

For two -equivalence classes 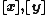of admissible sequences 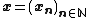and 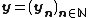we have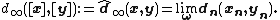

It is not hard to see that 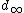is well-defined and that it is a metric on the set .

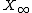Denote .

On basepoints in the case of uniformly bounded spaces

Suppose that (Xn,dn) is a sequence of metric spaces of uniformly bounded diameter, that is, there exists a real number C>0 such that diam(Xn)≤C for every 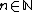. Then for any choice pn of base-points in Xn every sequence 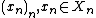is admissible. Therefore, in this situation the choice of base-points does not have to be specified when defining an ultralimit, and the ultralimit 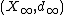depends only on (Xn,dn) and on ω but does not depend on the choice of a base-point sequence 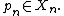. In this case one writes .

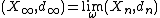Basic properties of ultralimits

  1. If (Xn,dn) are geodesic metric spaces then 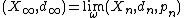is also a geodesic metric space.&91;1&93;
  2. If (Xn,dn) are complete metric spaces then is also a complete metric space.&91;2&93;&91;3&93;

Actually, by construction, the limit space is always complete, even when (Xn,dn)

is a repeating sequence of a space (X,d) which is not complete.[4]

  1. If (Xn,dn) are compact metric spaces that converge to a compact metric space (X,d) in the Gromov–Hausdorff sense (this automatically implies that the spaces (Xn,dn) have uniformly bounded diameter), then the ultralimit 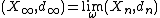is isometric to (X,d).
  2. Suppose that (Xn,dn) are proper metric spaces and that 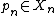are base-points such that the pointed sequence (Xn,dn,pn) converges to a proper metric space (X,d) in the Gromov–Hausdorff sense. Then the ultralimit 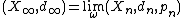is isometric to (X,d).&91;1&93;
  3. Let κ≤0 and let (Xn,dn) be a sequence of CAT(κ)-metric spaces. Then the ultralimit is also a CAT(κ)-space.&91;5&93;
  4. Let (Xn,dn) be a sequence of CAT(κn)-metric spaces where 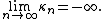Then the ultralimit is real tree.&91;5&93;

Asymptotic cones

An important class of ultralimits are the so-called asymptotic cones of metric spaces. Let (X,d) be a metric space, let ω be a non-principal ultrafilter on and let pn ∈ X be a sequence of base-points. Then the ω–ultralimit of the sequence 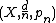is called the asymptotic cone of X with respect to ω and 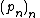and is denoted 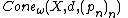. One often takes the base-point sequence to be constant, pn = p for some p ∈ X; in this case the asymptotic cone does not depend on the choice of p ∈ X and is denoted by 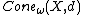or just .

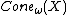The notion of an asymptotic cone plays an important role in geometric group theory since asymptotic cones (or, more precisely, their topological types and bi-Lipschitz types) provide quasi-isometry invariants of metric spaces in general and of finitely generated groups in particular.[6] Asymptotic cones also turn out to be a useful tool in the study of relatively hyperbolic groups and their generalizations.[7]

Examples

  1. Let (X,d) be a compact metric space and put (Xn,dn)=(X,d) for every 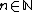. Then the ultralimit 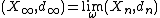is isometric to (X,d).
  2. Let (X,dX) and (Y,dY) be two distinct compact metric spaces and let (Xn,dn) be a sequence of metric spaces such that for each n either (Xn,dn)=(X,dX) or (Xn,dn)=(Y,dY). Let 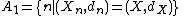and 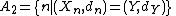. Thus A1, A2 are disjoint and 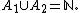Therefore, one of A1, A2 has ω-measure 1 and the other has ω-measure 0. Hence 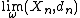is isometric to (X,dX) if ω(A1)=1 and 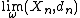is isometric to (Y,dY) if ω(A2)=1. This shows that the ultralimit can depend on the choice of an ultrafilter ω.
  3. Let (M,g) be a compact connected Riemannian manifold of dimension m, where g is a Riemannian metric on M. Let d be the metric on M corresponding to g, so that (M,d) is a geodesic metric space. Choose a basepoint p∈M. Then the ultralimit (and even the ordinary Gromov-Hausdorff limit) 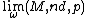is isometric to the tangent space TpM of M at p with the distance function on TpM given by the inner product g(p). Therefore, the ultralimit 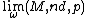is isometric to the Euclidean space 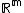with the standard Euclidean metric.&91;8&93;
  4. Let 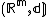be the standard m-dimensional Euclidean space with the standard Euclidean metric. Then the asymptotic cone 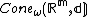is isometric to .
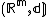  5. Let 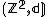be the 2-dimensional integer lattice where the distance between two lattice points is given by the length of the shortest edge-path between them in the grid. Then the asymptotic cone 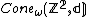is isometric to 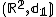where 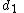is the Taxicab metric (or L1-metric) on .
  6. Let (X,d) be a δ-hyperbolic geodesic metric space for some δ≥0. Then the asymptotic cone 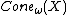is a real tree.&91;5&93;&91;9&93;
  7. Let (X,d) be a metric space of finite diameter. Then the asymptotic cone 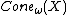is a single point.
  8. Let (X,d) be a CAT(0)-metric space. Then the asymptotic cone 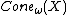is also a CAT(0)-space.&91;5&93;

Footnotes

1. ^John Roe. Lectures on Coarse Geometry. American Mathematical Society, 2003. {{isbn|978-0-8218-3332-2}}; Definition 7.19, p. 107.
2. ^L.Van den Dries, A.J.Wilkie, On Gromov's theorem concerning groups of polynomial growth and elementary logic. Journal of Algebra, Vol. 89(1984), pp. 349–374.
3. ^John Roe. Lectures on Coarse Geometry. American Mathematical Society, 2003. {{isbn|978-0-8218-3332-2}}; Proposition 7.20, p. 108.
4. ^Bridson, Haefliger "Metric Spaces of Non-positive curvature" Lemma 5.53
5. ^1 2 3 4 5 6 M. Kapovich B. Leeb. On asymptotic cones and quasi-isometry classes of fundamental groups of 3-manifolds, Geometric and Functional Analysis, Vol. 5 (1995), no. 3, pp. 582–603
6. ^John Roe. Lectures on Coarse Geometry. American Mathematical Society, 2003. {{isbn|978-0-8218-3332-2}}
7. ^Cornelia Druţu and Mark Sapir (with an Appendix by Denis Osin and Mark Sapir), Tree-graded spaces and asymptotic cones of groups. Topology, Volume 44 (2005), no. 5, pp. 959–1058.
8. ^Yu. Burago, M. Gromov, and G. Perel'man. A. D. Aleksandrov spaces with curvatures bounded below (in Russian), Uspekhi Matematicheskih Nauk vol. 47 (1992), pp. 3–51; translated in: Russian Math. Surveys vol. 47, no. 2 (1992), pp. 1–58
9. ^John Roe. Lectures on Coarse Geometry. American Mathematical Society, 2003. {{isbn|978-0-8218-3332-2}}; Example 7.30, p. 118.

Basic References

  • John Roe. Lectures on Coarse Geometry. American Mathematical Society, 2003. {{isbn|978-0-8218-3332-2}}; Ch. 7.
  • L.Van den Dries, A.J.Wilkie, On Gromov's theorem concerning groups of polynomial growth and elementary logic. Journal of Algebra, Vol. 89(1984), pp. 349–374.
  • M. Kapovich B. Leeb. On asymptotic cones and quasi-isometry classes of fundamental groups of 3-manifolds, Geometric and Functional Analysis, Vol. 5 (1995), no. 3, pp. 582–603
  • M. Kapovich. Hyperbolic Manifolds and Discrete Groups. Birkhäuser, 2000. {{isbn|978-0-8176-3904-4}}; Ch. 9.
  • Cornelia Druţu and Mark Sapir (with an Appendix by Denis Osin and Mark Sapir), Tree-graded spaces and asymptotic cones of groups. Topology, Volume 44 (2005), no. 5, pp. 959–1058.
  • M. Gromov. Metric Structures for Riemannian and Non-Riemannian Spaces. Progress in Mathematics vol. 152, Birkhäuser, 1999. {{isbn|0-8176-3898-9}}; Ch. 3.
  • B. Kleiner and B. Leeb, Rigidity of quasi-isometries for symmetric spaces and Euclidean buildings. Publications Mathématiques de L'IHÉS. Volume 86, Number 1, December 1997, pp. 115–197.

See also

  • Ultrafilter
  • Geometric group theory
  • Gromov-Hausdorff convergence

2 : Geometric group theory|Metric geometry
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/17 23:02:53