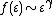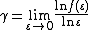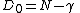- References
In mathematics, the uncertainty exponent is a method of measuring the fractal dimension of a basin boundary. In a chaotic scattering system, the
invariant set of the system is usually not directly accessible because it is non-attracting and typically of measure zero. Therefore, the only way to infer the presence of members
and to measure the properties of the invariant set is through the basins of attraction. Note that in a scattering system, basins of attraction are not limit cycles therefore do not constitute members of the invariant set.
Suppose we start with a random trajectory and perturb it by a small amount,
, in a random direction. If the new trajectory ends up
in a different basin from the old one, then it is called epsilon uncertain.
If we take a large number of such trajectories,
then the fraction of them that are epsilon uncertain is the uncertainty fraction,
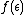, and we expect it to scale exponentially
with 
:
Thus the uncertainty exponent, 
, is defined as follows:
The uncertainty exponent can be shown to approximate the box-counting dimension
as follows:
where N is the embedding dimension. Please refer to the article on chaotic mixing for an example of numerical computation of the uncertainty dimension
compared with that of a box-counting dimension.
References
- C. Grebogi, S. W. McDonald, E. Ott and J. A. Yorke, Final state sensitivity: An obstruction to predictability, Phys. Letters 99A: 415-418 (1983).
- {{Cite book
| author = Edward Ott
| title = Chaos in Dynamical Systems
| publisher = Cambridge University Press
| year = 1993
}}