“Uncertainty theory”的意思、由来-开放百科全书

词条

Uncertainty theory

释义

Four axioms
Uncertain variables
Uncertainty distribution
Independence
Operational law
Expected Value
Variance
Critical value
Entropy
Inequalities
Convergence concept
Conditional uncertainty
References
Sources

{{distinguish|Uncertainty principle}}{{multiple issues|{{more footnotes|date=May 2018}}{{technical|date=December 2009}}{{howto|date=December 2009}}{{citation style|date=December 2009}}{{misleading|date=December 2009}}
}}Uncertainty theory is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms.{{Clarify|date=December 2009}} It was founded by Baoding Liu ^[1] in 2007 and refined in 2009.^[2]

Mathematical measures of the likelihood of an event being true include probability theory, capacity, fuzzy logic, possibility, and credibility, as well as uncertainty.

Four axioms

Axiom 1. (Normality Axiom) .

Axiom 2. (Self-Duality Axiom) .

Axiom 3. (Countable Subadditivity Axiom) For every countable sequence of events Λ₁, Λ₂, ..., we have

Axiom 4. (Product Measure Axiom) Let be uncertainty spaces for . Then the product uncertain measure is an uncertain measure on the product σ-algebra satisfying

Principle. (Maximum Uncertainty Principle) For any event, if there are multiple reasonable values that an uncertain measure may take, then the value as close to 0.5 as possible is assigned to the event.

Uncertain variables

An uncertain variable is a measurable function ξ from an uncertainty space to the set of real numbers, i.e., for any Borel set B of real numbers, the set

is an event.

Uncertainty distribution

Uncertainty distribution is inducted to describe uncertain variables.

Definition:The uncertainty distribution of an uncertain variable ξ is defined by .

Theorem(Peng and Iwamura, Sufficient and Necessary Condition for Uncertainty Distribution) A function is an uncertain distribution if and only if it is an increasing function except and .

Independence

Definition: The uncertain variables are said to be independent if

for any Borel sets of real numbers.

Theorem 1: The uncertain variables are independent if

for any Borel sets of real numbers.

Theorem 2: Let be independent uncertain variables, and measurable functions. Then are independent uncertain variables.

Theorem 3: Let be uncertainty distributions of independent uncertain variables respectively, and the joint uncertainty distribution of uncertain vector . If are independent, then we have

for any real numbers .

Operational law

Theorem: Let be independent uncertain variables, and a measurable function. Then is an uncertain variable such that

where are Borel sets, and means for any.

Expected Value

Definition: Let be an uncertain variable. Then the expected value of is defined by

provided that at least one of the two integrals is finite.

Theorem 1: Let be an uncertain variable with uncertainty distribution . If the expected value exists, then

Theorem 2: Let be an uncertain variable with regular uncertainty distribution . If the expected value exists, then

Theorem 3: Let and be independent uncertain variables with finite expected values. Then for any real numbers and , we have

Variance

Definition: Let be an uncertain variable with finite expected value . Then the variance of is defined by

Theorem: If be an uncertain variable with finite expected value, and are real numbers, then

Critical value

Definition: Let be an uncertain variable, and . Then

is called the α-optimistic value to , and

is called the α-pessimistic value to .

Theorem 1: Let be an uncertain variable with regular uncertainty distribution . Then its α-optimistic value and α-pessimistic value are

Theorem 2: Let be an uncertain variable, and . Then we have

if , then ;
if , then .

Theorem 3: Suppose that and are independent uncertain variables, and . Then we have

Entropy

Definition: Let be an uncertain variable with uncertainty distribution . Then its entropy is defined by

where .

Theorem 1(Dai and Chen): Let be an uncertain variable with regular uncertainty distribution . Then

Theorem 2: Let and be independent uncertain variables. Then for any real numbers and , we have

Theorem 3: Let be an uncertain variable whose uncertainty distribution is arbitrary but the expected value and variance . Then

Inequalities

Theorem 1(Liu, Markov Inequality): Let be an uncertain variable. Then for any given numbers and 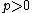, we have

Theorem 2 (Liu, Chebyshev Inequality) Let be an uncertain variable whose variance exists. Then for any given number, we have

Theorem 3 (Liu, Holder’s Inequality) Let and be positive numbers with , and let and be independent uncertain variables with and . Then we have

Theorem 4:(Liu [127], Minkowski Inequality) Let be a real number with , and let and be independent uncertain variables with and . Then we have

Convergence concept

Definition 1: Suppose that are uncertain variables defined on the uncertainty space . The sequence is said to be convergent a.s. to if there exists an event with such that

for every . In that case we write ,a.s.

Definition 2: Suppose that are uncertain variables. We say that the sequence converges in measure to if

for every .

Definition 3: Suppose that are uncertain variables with finite expected values. We say that the sequence converges in mean to if

Definition 4: Suppose that are uncertainty distributions of uncertain variables , respectively. We say that the sequence converges in distribution to if at any continuity point of .

Theorem 1: Convergence in Mean Convergence in Measure Convergence in Distribution.

However, Convergence in Mean 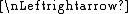Convergence Almost Surely 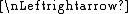Convergence in Distribution.

Conditional uncertainty

Definition 1: Let be an uncertainty space, and . Then the conditional uncertain measure of A given B is defined by

Theorem 1: Let be an uncertainty space, and B an event with . Then M{·|B} defined by Definition 1 is an uncertain measure, and is an uncertainty space.

Definition 2: Let be an uncertain variable on . A conditional uncertain variable of given B is a measurable function from the conditional uncertainty space to the set of real numbers such that

Definition 3: The conditional uncertainty distribution of an uncertain variable given B is defined by

provided that .

Theorem 2: Let be an uncertain variable with regular uncertainty distribution , and a real number with . Then the conditional uncertainty distribution of given is

Theorem 3: Let be an uncertain variable with regular uncertainty distribution , and a real number with . Then the conditional uncertainty distribution of given is

Definition 4: Let be an uncertain variable. Then the conditional expected value of given B is defined by

provided that at least one of the two integrals is finite.

References

1. ^Baoding Liu, Uncertainty Theory, 2nd ed., Springer-Verlag, Berlin, 2007.
2. ^Baoding Liu, Uncertainty Theory, 4th ed., http://orsc.edu.cn/liu/ut.pdf.

Sources

Xin Gao, Some Properties of Continuous Uncertain Measure, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol.17, No.3, 419-426, 2009.
Cuilian You, Some Convergence Theorems of Uncertain Sequences, Mathematical and Computer Modelling, Vol.49, Nos.3-4, 482-487, 2009.
Yuhan Liu, How to Generate Uncertain Measures, Proceedings of Tenth National Youth Conference on Information and Management Sciences, August 3–7, 2008, Luoyang, pp. 23–26.
Baoding Liu, Some Research Problems in Uncertainty Theory, Journal of Uncertain Systems, Vol.3, No.1, 3-10, 2009.
Yang Zuo, Xiaoyu Ji, Theoretical Foundation of Uncertain Dominance, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 827–832.
Yuhan Liu and Minghu Ha, Expected Value of Function of Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 779–781.
Zhongfeng Qin, On Lognormal Uncertain Variable, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 753–755.
Jin Peng, Value at Risk and Tail Value at Risk in Uncertain Environment, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 787–793.
Yi Peng, U-Curve and U-Coefficient in Uncertain Environment, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 815–820.
Wei Liu, Jiuping Xu, Some Properties on Expected Value Operator for Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 808–811.
Xiaohu Yang, Moments and Tails Inequality within the Framework of Uncertainty Theory, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 812–814.
Yuan Gao, Analysis of k-out-of-n System with Uncertain Lifetimes, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 794–797.
Xin Gao, Shuzhen Sun, Variance Formula for Trapezoidal Uncertain Variables, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 853–855.
Zixiong Peng, A Sufficient and Necessary Condition of Product Uncertain Null Set, Proceedings of the Eighth International Conference on Information and Management Sciences, Kunming, China, July 20–28, 2009, pp. 798–801.

2 : Probability theory|Fuzzy logic

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。