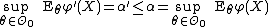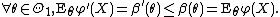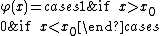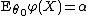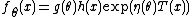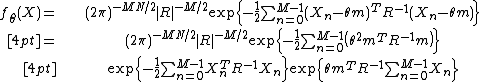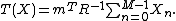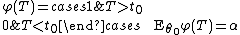“Uniformly most powerful test”的意思、由来-开放百科全书

词条

Uniformly most powerful test

释义

Setting
Formal definition
The Karlin–Rubin theorem
Important case: exponential family
Example
Further discussion
References
Further reading

In statistical hypothesis testing, a uniformly most powerful (UMP) test is a hypothesis test which has the greatest power among all possible tests of a given size α. For example, according to the Neyman–Pearson lemma, the likelihood-ratio test is UMP for testing simple (point) hypotheses.

Setting

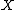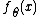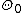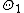Let denote a random vector (corresponding to the measurements), taken from a parametrized family of probability density functions or probability mass functions , which depends on the unknown deterministic parameter . The parameter space is partitioned into two disjoint sets and . Let 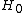denote the hypothesis that 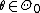, and let denote the hypothesis that .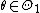

The binary test of hypotheses is performed using a test function .

meaning that is in force if the measurement 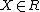and that 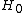is in force if the measurement .

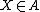Note that 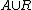is a disjoint covering of the measurement space.

Formal definition

A test function is UMP of size if for any other test function 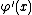satisfying

we have

The Karlin–Rubin theorem

The Karlin–Rubin theorem can be regarded as an extension of the Neyman–Pearson lemma for composite hypotheses.^[1] Consider a scalar measurement having a probability density function parameterized by a scalar parameter θ, and define the likelihood ratio .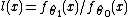

If 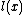is monotone non-decreasing, in , for any pair 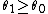(meaning that the greater is, the more likely is), then the threshold test:

where is chosen such that

is the UMP test of size α for testing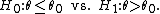

Note that exactly the same test is also UMP for testing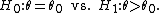

Important case: exponential family

Although the Karlin-Rubin theorem may seem weak because of its restriction to scalar parameter and scalar measurement, it turns out that there exist a host of problems for which the theorem holds. In particular, the one-dimensional exponential family of probability density functions or probability mass functions with

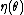has a monotone non-decreasing likelihood ratio in the sufficient statistic , provided that is non-decreasing.

Example

Let 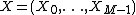denote i.i.d. normally distributed -dimensional random vectors with mean 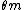and covariance matrix . We then have

which is exactly in the form of the exponential family shown in the previous section, with the sufficient statistic being

Thus, we conclude that the test

is the UMP test of size for testing vs.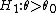

Further discussion

Finally, we note that in general, UMP tests do not exist for vector parameters or for two-sided tests (a test in which one hypothesis lies on both sides of the alternative). The reason is that in these situations, the most powerful test of a given size for one possible value of the parameter (e.g. for 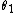where 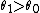) is different from the most powerful test of the same size for a different value of the parameter (e.g. for 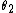where 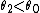). As a result, no test is uniformly most powerful in these situations.

References

1. ^Casella, G.; Berger, R.L. (2008), Statistical Inference, Brooks/Cole. {{ISBN|0-495-39187-5}} (Theorem 8.3.17)