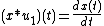- References
In mathematics, the unit doublet is the derivative of the Dirac delta function. It can be used to differentiate signals in electrical engineering:[1] If u1 is the unit doublet, then
where  is the convolution operator.[2]
is the convolution operator.[2]
The function is zero for all values except zero, where its behaviour is interesting. Its integral over any interval enclosing zero is zero. However, the integral of its absolute value over any region enclosing zero goes to infinity. The function can be thought of as the limiting case of two rectangles, one in the second quadrant, and the other in the fourth. The length of each rectangle is k, whereas their breadth is 1/k2, where k tends to zero.
References
1. ^{{cite web|url=http://ocw.mit.edu/NR/rdonlyres/Electrical-Engineering-and-Computer-Science/6-003Fall-2003/9BEA2A94-230F-4F38-ABAE-F552B8E549A9/0/lecture4.pdf|title=Signals and Systems Lecture #4|date=16 September 2003|work=Mit.edu|accessdate=2 September 2009|deadurl=yes|archiveurl=https://web.archive.org/web/20090219052652/http://ocw.mit.edu/NR/rdonlyres/Electrical-Engineering-and-Computer-Science/6-003Fall-2003/9BEA2A94-230F-4F38-ABAE-F552B8E549A9/0/lecture4.pdf|archivedate=19 February 2009|df=}}
2. ^http://isites.harvard.edu/fs/docs/icb.topic133182.files/5-singular_func.pdf
{{DEFAULTSORT:Unit Doublet}}{{mathanalysis-stub}}2. ^http://isites.harvard.edu/fs/docs/icb.topic133182.files/5-singular_func.pdf
1 : Generalized functions
- Discovery Channel Networks International
- Discovery Channel Norway
- Discovery Channel Sweden
- Discovery Channel (UK and Ireland)
- Discovery College
- Discovery Communications
- Discovery Communications Asia
- Discovery Communications Inc.
- Discovery Communications India
- Discovery Day and National Youth Day
- Discovery & Development Services
- Discovery District-Columbus, Ohio
- Discovery District (Columbus, Ohio)
- Discovery Expedition (clothing)
- Discovery Family (France)
- Discovery Harbour, Hawaii
- Discovery HD World
- Discovery High School (Georgia)
- Discovery High School (Lawrenceville)
- Discovery High Schools
- Discovery Hill
- Discovery Hill (Sagamore, Massachusetts)
- Discovery Hill (Sandwich, Massachusetts)
- Discovery Home and Health Southeast Asia
- Discovery hotspot