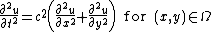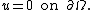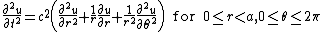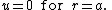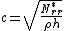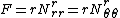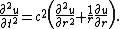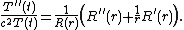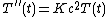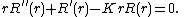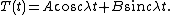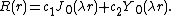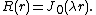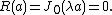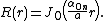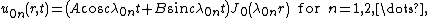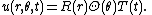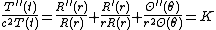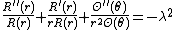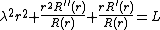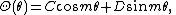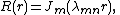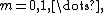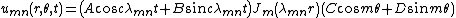- Motivation
- The problem
- The axisymmetric case
- The general case
- Animations of several vibration modes
- See also
- References
A two-dimensional elastic membrane under tension can support transverse vibrations. The properties of an idealized drumhead can be modeled by the vibrations of a circular membrane of uniform thickness, attached to a rigid frame. Due to the phenomenon of resonance, at certain vibration frequencies, its resonant frequencies, the membrane can store vibrational energy, the surface moving in a characteristic pattern of standing waves. This is called a normal mode. A membrane has an infinite number of these normal modes, starting with a lowest frequency one called the fundamental mode.
There exist infinitely many ways in which a membrane can vibrate, each depending on the shape of the membrane at some initial time, and the transverse velocity of each point on the membrane at that time. The vibrations of the membrane are given by the solutions of the two-dimensional wave equation with Dirichlet boundary conditions which represent the constraint of the frame. It can be shown that any arbitrarily complex vibration of the membrane can be decomposed into a possibly infinite series of the membrane's normal modes. This is analogous to the decomposition of a time signal into a Fourier series.
The study of vibrations on drums led mathematicians to pose a famous mathematical problem on whether the shape of a drum can be heard, with an answer being given in 1992 in the two-dimensional setting.
Motivation
Analyzing the vibrating drum head problem explains percussion instruments such as drums and timpani. However, there is also a biological application in the working of the eardrum. From an educational point of view the modes of a two-dimensional object are a convenient way to visually demonstrate the meaning of modes, nodes, antinodes and even quantum numbers. These concepts are important to the understanding of the structure of the atom.
The problem
Consider an open disk  of radius
of radius  centered at the origin, which will represent the "still" drum head shape. At any time
centered at the origin, which will represent the "still" drum head shape. At any time  the height of the drum head shape at a point
the height of the drum head shape at a point  in
in  measured from the "still" drum head shape will be denoted by
measured from the "still" drum head shape will be denoted by  which can take both positive and negative values. Let
which can take both positive and negative values. Let  denote the boundary of
denote the boundary of  that is, the circle of radius
that is, the circle of radius  centered at the origin, which represents the rigid frame to which the drum head is attached.
centered at the origin, which represents the rigid frame to which the drum head is attached.
The mathematical equation that governs the vibration of the drum head is the wave equation with zero boundary conditions,
Due to the circular geometry of  , it will be convenient to use cylindrical coordinates,
, it will be convenient to use cylindrical coordinates, 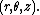 Then, the above equations are written as
Then, the above equations are written as
Here,  is a positive constant, which gives the speed at which transverse vibration waves propagate in the membrane. In terms of the physical parameters, the wave speed, c, is given by
is a positive constant, which gives the speed at which transverse vibration waves propagate in the membrane. In terms of the physical parameters, the wave speed, c, is given by
where 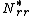 , is the radial membrane resultant at the membrane boundary (
, is the radial membrane resultant at the membrane boundary ( ),
),  , is the membrane thickness, and
, is the membrane thickness, and  is the membrane density. If the membrane has uniform tension, the uniform tension force at a given radius,
is the membrane density. If the membrane has uniform tension, the uniform tension force at a given radius,  may be written
may be written
where 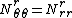 is the membrane resultant in the azimuthal direction.
is the membrane resultant in the azimuthal direction.
The axisymmetric case
We will first study the possible modes of vibration of a circular drum head that are axisymmetric. Then, the function  does not depend on the angle
does not depend on the angle  and the wave equation simplifies to
and the wave equation simplifies to
We will look for solutions in separated variables, 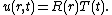 Substituting this in the equation above and dividing both sides by
Substituting this in the equation above and dividing both sides by 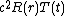 yields
yields
The left-hand side of this equality does not depend on 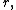 and the right-hand side does not depend on
and the right-hand side does not depend on 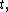 it follows that both sides must be equal to some constant
it follows that both sides must be equal to some constant 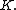 We get separate equations for
We get separate equations for  and
and 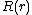 :
:
The equation for  has solutions which exponentially grow or decay for
has solutions which exponentially grow or decay for 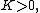 are linear or constant for
are linear or constant for 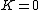 and are periodic for
and are periodic for 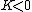 . Physically it is expected that a solution to the problem of a vibrating drum head will be oscillatory in time, and this leaves only the third case,
. Physically it is expected that a solution to the problem of a vibrating drum head will be oscillatory in time, and this leaves only the third case, 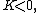 when
when 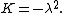 Then,
Then,  is a linear combination of sine and cosine functions,
is a linear combination of sine and cosine functions,
Turning to the equation for 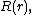 with the observation that
with the observation that 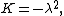 all solutions of this second-order differential equation are a linear combination of Bessel functions of order 0, since this is a special case of Bessel's differential equation:
all solutions of this second-order differential equation are a linear combination of Bessel functions of order 0, since this is a special case of Bessel's differential equation:
The Bessel function 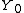 is unbounded for
is unbounded for 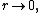 which results in an unphysical solution to the vibrating drum head problem, so the constant
which results in an unphysical solution to the vibrating drum head problem, so the constant  must be null. We will also assume
must be null. We will also assume 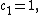 as otherwise this constant can be absorbed later into the constants
as otherwise this constant can be absorbed later into the constants  and
and  coming from
coming from 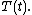 It follows that
It follows that
The requirement that height  be zero on the boundary of the drum head results in the condition
be zero on the boundary of the drum head results in the condition
The Bessel function  has an infinite number of positive roots,
has an infinite number of positive roots,
We get that 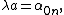 for
for 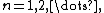 so
so
Therefore, the axisymmetric solutions  of the vibrating drum head problem that can be represented in separated variables are
of the vibrating drum head problem that can be represented in separated variables are
where 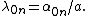
The general case
The general case, when  can also depend on the angle
can also depend on the angle  is treated similarly. We assume a solution in separated variables,
is treated similarly. We assume a solution in separated variables,
Substituting this into the wave equation and separating the variables, gives
where  is a constant. As before, from the equation for
is a constant. As before, from the equation for  it follows that
it follows that 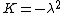 with
with 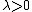 and
and
From the equation
we obtain, by multiplying both sides by  and separating variables, that
and separating variables, that
and
for some constant  Since
Since 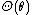 is periodic, with period
is periodic, with period 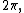
 being an angular variable, it follows that
being an angular variable, it follows that
where 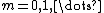 and
and  and
and  are some constants. This also implies
are some constants. This also implies 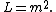
Going back to the equation for 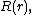 its solution is a linear combination of Bessel functions
its solution is a linear combination of Bessel functions 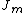 and
and 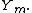 With a similar argument as in the previous section, we arrive at
With a similar argument as in the previous section, we arrive at
where 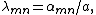 with
with 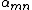 the
the  -th positive root of
-th positive root of 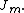
We showed that all solutions in separated variables of the vibrating drum head problem are of the form
for 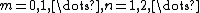
Animations of several vibration modes
A number of modes are shown below together with their quantum numbers. The analogous wave functions of the hydrogen atom are also indicated as well as the associated angular frequency 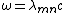 .
.
See also
- Vibrating string, the one-dimensional case
- Chladni patterns, an early description of a related phenomenon, in particular with musical instruments; see also cymatics
- Hearing the shape of a drum, characterising the modes with respect to the shape of the membrane
- Atomic orbital, a related quantum-mechanical and three-dimensional problem
References
- {{Cite book | author=H. Asmar, Nakhle | authorlink= | coauthors= | title=Partial differential equations with Fourier series and boundary value problems | year=2005 | publisher=Pearson Prentice Hall | location=Upper Saddle River, N.J. | isbn=0-13-148096-0 | page=198}}
- BDO British Open
- Bdo canadian open of curling
- BDO Classic Canadian Open
- BDO (disambiguation)
- BDO Dunwoody
- Bdo dunwoody
- BDO Dutch Masters
- BDO Grand Slam
- BDO International Open
- BDO International Open (darts)
- Bdo kendalls
- BDO Kendalls
- B. Dolan
- B dolan
- BDO Russia
- B'dos Jazz Festival
- BDO Stoy Hayward
- B-double
- B-double-flat major
- B-double-flat minor
- B. D. Owens
- BDO World Championships
- BDO World Darts Championship 2010
- BDP1
- BDP Architects