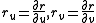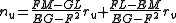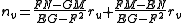“Weingarten equations”的意思、由来-开放百科全书

词条

Weingarten equations

释义

Statement in classical differential geometry
Notes
References

Weingarten equations give expansion of the derivative of the unit normal vector to a surface in terms of the first derivatives of the position vector of this surface. These formulas were established in 1861 by German mathematician Julius Weingarten.^[1]

Statement in classical differential geometry

Let S be a surface in three-dimensional Euclidean space that is parametrized by position vector r(u, v) of the surface. Let P = P(u, v) be a fixed point on this surface. Then

are two tangent vectors at point P.

Let n be the unit normal vector and let (E, F, G) and (L, M, N) be the coefficients of the first and second fundamental forms of this surface, respectively. The Weingarten equation gives the first derivative of the unit normal vector n at point P in terms of tangent vectors r_u and r_v:

This can be expressed compactly in index notation as

,

where K_ab are the components of the surface's curvature tensor.

Notes

1. ^{{cite journal|author=J. Weingarten|journal=Journal für die Reine und Angewandte Mathematik |title=Ueber eine Klasse auf einander abwickelbarer Flächen|volume=59|year=1861|pages=382–393}}

References

{{MathWorld|urlname=WeingartenEquations|title=Weingarten Equations}}
Springer Encyclopedia of Mathematics, Weingarten derivational formulas
{{citation|last1 = Struik|first1=Dirk J.|title=Lectures on Classical Differential Geometry|year = 1988|publisher = Dover Publications|page=108|isbn=0-486-65609-8}}
Erwin Kreyszig, Differential Geometry, Dover Publications, 1991, {{isbn|0-486-66721-9}}, section 45.

1 : Differential geometry of surfaces

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。