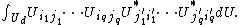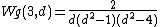“Weingarten function”的意思、由来-开放百科全书

词条

Weingarten function

释义

Unitary groups
Examples Asymptotic behavior
Orthogonal and symplectic groups
External links
References

In mathematics, Weingarten functions are rational functions indexed by partitions of integers that can be used to calculate integrals of products of matrix coefficients over classical groups. They were first studied by {{harvtxt|Weingarten|1978}} who found their asymptotic behavior, and named by {{harvtxt|Collins|2003}}, who evaluated them explicitly for the unitary group.

Unitary groups

Weingarten functions are used for evaluating integrals over the unitary group U_d

of products of matrix coefficients of the form

(Here denotes the conjugate transpose of , alternatively denoted as .)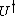

This integral is equal to

where Wg is the Weingarten function, given by

where the sum is over all partitions λ of q {{harv|Collins|2003}}. Here χ^λ is the character of S_q corresponding to the partition λ and s is the Schur polynomial of λ, so that s_λd(1) is the dimension of the representation of U_d corresponding to λ.

The Weingarten functions are rational functions in d. They can have poles for small values of d, which cancel out in the formula above. There is an alternative inequivalent definition of Weingarten functions, where one only sums over partitions with at most d parts. This is no longer a rational function of d, but is finite for all positive integers d. The two sorts of Weingarten functions coincide for d larger than q, and either can be used in the formula for the integral.

Examples

The first few Weingarten functions Wg(σ, d) are

(The trivial case where q = 0)

where permutations σ are denoted by their cycle shapes.

There exist computer algebra programs to produce these expressions.^[1]^[2]

Asymptotic behavior

For large d, the Weingarten function Wg has the asymptotic behavior

where the permutation σ is a product of cycles of lengths C_i, and c_n = (2n)!/n!(n + 1)! is a Catalan number, and |σ| is the smallest number of transpositions that σ is a product of. There exists a diagrammatic method^[3] to systematically calculate the integrals over the unitary group as a power series in 1/d.

Orthogonal and symplectic groups

For orthogonal and symplectic groups the Weingarten functions were evaluated by {{harvtxt|Collins|Śniady|2006}}. Their theory is similar to the case of the unitary group. They are parameterized by partitions such that all parts have even size.

External links

{{Citation | last1=Collins | first1=Benoît | title=Moments and cumulants of polynomial random variables on unitary groups, the Itzykson-Zuber integral, and free probability | arxiv=math-ph/0205010 | doi=10.1155/S107379280320917X | mr=1959915 | year=2003 | journal=International Mathematics Research Notices | issue=17 | pages=953–982 | volume=2003}}
{{Citation | last1=Collins | first1=Benoît | last2=Śniady | first2=Piotr | title=Integration with respect to the Haar measure on unitary, orthogonal and symplectic group | doi=10.1007/s00220-006-1554-3 | mr=2217291 | year=2006 | journal=Communications in Mathematical Physics | volume=264 | issue=3 | pages=773–795| arxiv=math-ph/0402073 | bibcode=2006CMaPh.264..773C }}
{{Citation | last1=Weingarten | first1=Don | title=Asymptotic behavior of group integrals in the limit of infinite rank | doi=10.1063/1.523807 | mr=0471696 | year=1978 | journal=Journal of Mathematical Physics | volume=19 | issue=5 | pages=999–1001| bibcode=1978JMP....19..999W }}

References

1. ^Z. Puchała and J.A. Miszczak, [https://arxiv.org/abs/1109.4244 Symbolic integration with respect to the Haar measure on the unitary group in Mathematica.], arXiv:1109.4244 (2011).
2. ^M. Fukuda, R. König, and I. Nechita, [https://arxiv.org/abs/1902.08539 RTNI - A symbolic integrator for Haar-random tensor networks.], arXiv:1902.08539 (2019).
3. ^P.W. Brouwer and C.W.J. Beenakker, [https://arxiv.org/abs/cond-mat/9604059 Diagrammatic method of integration over the unitary group, with applications to quantum transport in mesoscopic systems], J. Math. Phys. 37, 4904 (1996), arXiv:cond-mat/9604059.

2 : Random matrices|Mathematical physics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。