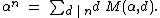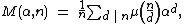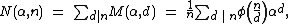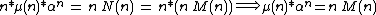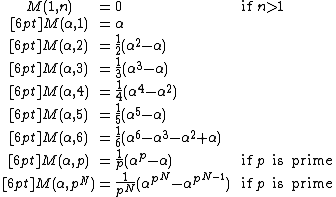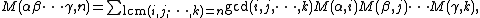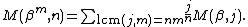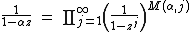“Necklace polynomial”的意思、由来-开放百科全书

词条

Necklace polynomial

释义

Relations between M and N
Examples
Identities
Cyclotomic identity
Applications
References

In combinatorial mathematics, the necklace polynomial, or Moreau's necklace-counting function, introduced by {{harvs|txt|authorlink=Charles Paul Narcisse Moreau|first=C.|last=Moreau|year=1872}}, is the family of polynomials 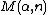in the variable such that

By Möbius inversion they are given by

where is the classic Möbius function.

A closely related family, called the general necklace polynomial or general necklace-counting function, is:

where is Euler's totient function.

Relations between M and N

The above formulas are easily related in terms of Dirichlet convolution of arithmetic functions 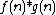, regarding as a constant.

The formula for M gives ,
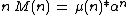The formula for N gives .
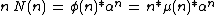Their relation gives 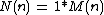or equivalently 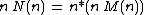, since n is completely multiplicative.

Any two of these imply the third, for example:

by cancellation in the Dirichlet algebra.

Examples

Identities

The polynomials obey various combinatorial identities, given by Metropolis & Rota:

where "gcd" is greatest common divisor and "lcm" is least common multiple. More generally,

which also implies:

Cyclotomic identity

Applications

The necklace polynomials 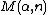appear as:

The number of aperiodic necklaces (or equivalently Lyndon words) which can be made by arranging n colored beads having α available colors. Two such necklaces are considered equal if they are related by a rotation (but not a reflection). Aperiodic refers to necklaces without rotational symmetry, having n distinct rotations. The polynomials 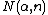give the number of necklaces including the periodic ones: this is easily computed using Polya theory.
The dimension of the degree n piece of the free Lie algebra on α generators ("Witt's formula"^[1]). Here 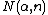should be the dimension of the degree n piece of the corresponding free Jordan algebra.
The number of monic irreducible polynomials of degree n over a finite field with α elements (when 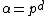is a prime power). Here 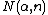is the number of polynomials which are primary (a power of an irreducible).
The exponent in the cyclotomic identity.

References

1. ^{{cite book | last=Lothaire | first=M. | authorlink=M. Lothaire | others=Perrin, D.; Reutenauer, C.; Berstel, J.; Pin, J. E.; Pirillo, G.; Foata, D.; Sakarovitch, J.; Simon, I.; Schützenberger, M. P.; Choffrut, C.; Cori, R.; Lyndon, Roger; Rota, Gian-Carlo. Foreword by Roger Lyndon | title=Combinatorics on words | edition=2nd | series=Encyclopedia of Mathematics and Its Applications | volume=17 | publisher=Cambridge University Press | year=1997 | isbn=978-0-521-59924-5 | zbl=0874.20040 | mr = 1475463 | pages=79,84 }}

{{citation | last1=Moreau | first1=C. |authorlink=Charles Paul Narcisse Moreau | title=Sur les permutations circulaires distinctes (On distinct circular permutations) | url=http://www.numdam.org/item?id=NAM_1872_2_11__309_0 | language=French | jfm=04.0086.01 | year=1872 | journal=Nouvelles Annales de Mathématiques, Journal des Candidats Aux écoles Polytechnique et Normale, Sér. 2 | volume=11 | pages=309–31}}

{{Citation | last1=Metropolis | first1=N. | author1-link=Nicholas Metropolis | last2=Rota | first2=Gian-Carlo | author2-link=Gian-Carlo Rota | title=Witt vectors and the algebra of necklaces | doi=10.1016/0001-8708(83)90035-X | mr=723197 | zbl=0545.05009 | year=1983 | journal=Advances in Mathematics | issn=0001-8708 | volume=50 | issue=2 | pages=95–125 | url = https://www.sciencedirect.com/science/article/pii/000187088390035X/pdf?md5=3cfd1a39f5235b827cb18f8a3e99ccc2&pid=1-s2.0-000187088390035X-main.pdf

}}

{{cite journal |last1=Reutenauer |first1=Christophe |title=Mots circulaires et polynomies irreductibles |journal=Ann. Sc. Math. Quebec |date=1988 |volume=12 |issue=2 |pages=275–285}}

2 : Combinatorics on words|Enumerative combinatorics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。