“Nest algebra”的意思、由来-开放百科全书

词条

Nest algebra

释义

Properties
See also
References

In functional analysis, a branch of mathematics, nest algebras are a class of operator algebras that generalise the upper-triangular matrix algebras to a Hilbert space context. They were introduced by {{harvs|txt|authorlink=John Ringrose|last=Ringrose|year=1965}} and have many interesting properties. They are non-selfadjoint algebras, are closed in the weak operator topology and are reflexive.

Nest algebras are among the simplest examples of commutative subspace lattice algebras. Indeed, they are formally defined as the algebra of bounded operators leaving invariant each subspace contained in a subspace nest, that is, a set of subspaces which is totally ordered by inclusion and is also a complete lattice. Since the orthogonal projections corresponding to the subspaces in a nest commute, nests are commutative subspace lattices.

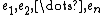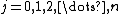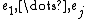By way of an example, let us apply this definition to recover the finite-dimensional upper-triangular matrices. Let us work in the -dimensional complex vector space , and let be the standard basis. For , let be the -dimensional subspace of spanned by the first basis vectors . Let

then N is a subspace nest, and the corresponding nest algebra of n × n complex matrices M leaving each subspace in N invariant that is, satisfying 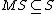for each S in N – is precisely the set of upper-triangular matrices.

If we omit one or more of the subspaces S_j from N then the corresponding nest algebra consists of block upper-triangular matrices.

Properties

Nest algebras are hyperreflexive with distance constant 1.

References

{{Citation | last1=Ringrose | first1=John R. | title=On some algebras of operators | doi=10.1112/plms/s3-15.1.61 |mr=0171174 | year=1965 | journal=Proceedings of the London Mathematical Society |series=Third Series | issn=0024-6115 | volume=15 | pages=61–83}}

2 : Operator theory|Operator algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Properties

See also

References