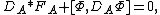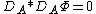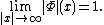“Yang–Mills–Higgs equations”的意思、由来-开放百科全书

词条

Yang–Mills–Higgs equations

释义

References

In mathematics, the Yang–Mills–Higgs equations are a set of non-linear partial differential equations for a Yang–Mills field, given by a connection, and a Higgs field, given by a section of a vector bundle. These equations are

with a boundary condition

These equations are named after Chen Ning Yang, Robert Mills, and Peter Higgs.

M.V. Goganov and L.V. Kapitanskii have shown that the Cauchy problem for hyperbolic Yang–Mills–Higgs equations in Hamiltonian gauge on 4-dimensional Minkowski space have a unique global solution with no restrictions at the spatial infinity. Furthermore, the solution has the finite propagation speed property.

References

M.V. Goganov and L.V. Kapitansii, "Global solvability of the initial problem for Yang-Mills-Higgs equations", Zapiski LOMI 147,18-48, (1985); J. Sov. Math, 37, 802-822 (1987).

1 : Partial differential equations

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。