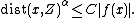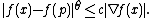“Łojasiewicz inequality”的意思、由来-开放百科全书

词条

Łojasiewicz inequality

释义

References

In real algebraic geometry, the Łojasiewicz inequality, named after Stanisław Łojasiewicz, gives an upper bound for the distance of a point to the nearest zero of a given real analytic function. Specifically, let ƒ : U → R be a real analytic function on an open set U in Rⁿ, and let Z be the zero locus of ƒ. Assume that Z is not empty. Then for any compact set K in U, there exist positive constants α and C such that, for all x in K

Here α can be large.

The following form of this inequality is often seen in more analytic contexts: with the same assumptions on ƒ, for every p ∈ U there is a possibly smaller open neighborhood W of p and constants θ ∈ (0,1) and c > 0 such that

References

{{Citation | last1=Bierstone | first1=Edward | last2=Milman | first2=Pierre D. | title=Semianalytic and subanalytic sets |mr=972342 | year=1988 | journal=Publications Mathématiques de l'IHÉS | issn=1618-1913 | issue=67 | pages=5–42|url=http://www.numdam.org/item?id=PMIHES_1988__67__5_0}}
{{Citation | doi=10.2307/2153965 | last1=Ji | first1=Shanyu | last2=Kollár | first2=János | last3=Shiffman | first3=Bernard | title=A global Łojasiewicz inequality for algebraic varieties |mr=1046016 | url=http://www.ams.org/journals/tran/1992-329-02/S0002-9947-1992-1046016-6/ | year=1992 | journal=Transactions of the American Mathematical Society | issn=0002-9947 | volume=329 | issue=2 | pages=813–818 | jstor=2153965}}

3 : Inequalities|Mathematical analysis|Real algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。