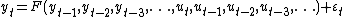“Nonlinear autoregressive exogenous model”的意思、由来-开放百科全书

词条

Nonlinear autoregressive exogenous model

释义

References
External links

In time series modeling, a nonlinear autoregressive exogenous model (NARX) is a nonlinear autoregressive model which has exogenous inputs. This means that the model relates the current value of a time series to both:

past values of the same series; and
current and past values of the driving (exogenous) series — that is, of the externally determined series that influences the series of interest.

In addition, the model contains:

an "error" term

which relates to the fact that knowledge of other terms will not enable the current value of the time series to be predicted exactly.

Such a model can be stated algebraically as

Here y is the variable of interest, and u is the externally determined variable. In this scheme, information about u helps predict y, as do previous values of y itself. Here ε is the error term (sometimes called noise). For example, y may be air temperature at noon, and u may be the day of the year (day-number within year).

The function F is some nonlinear function, such as a polynomial. F can be a neural network, a wavelet network, a sigmoid network and so on. To test for non-linearity in a time series, the BDS test (Brock-Dechert-Scheinkman test) developed for econometrics can be used.

References

S. A. Billings. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains, Wiley, {{ISBN|978-1-1199-4359-4}}, 2013.
I.J. Leontaritis and S.A. Billings. "Input-output parametric models for non-linear systems. Part I: deterministic non-linear systems". Int'l J of Control 41:303-328, 1985.
I.J. Leontaritis and S.A. Billings. "Input-output parametric models for non-linear systems. Part II: stochastic non-linear systems". Int'l J of Control 41:329-344, 1985.
O. Nelles. "Nonlinear System Identification". Springer Berlin, {{ISBN|3-540-67369-5}}, 2000.
W.A. Brock, J.A. Scheinkman, W.D. Dechert and B. LeBaron. "A Test for Independence based on the Correlation Dimension". Econometric Reviews 15:197-235, 1996.

External links

Open-source implementation of the NARX model using neural networks

2 : Time series models|Nonlinear time series analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。