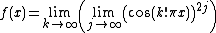1. Dirichlet function

2. Hyperreal characterisation

3. See also

4. References

5. External links

In mathematics, a nowhere continuous function, also called an everywhere discontinuous function, is a function that is not continuous at any point of its domain. If f is a function from real numbers to real numbers, then f is nowhere continuous if for each point x there is an {{nowrap|ε > 0}} such that for each {{nowrap|δ > 0}} we can find a point y such that {{nowrap|0 < {{abs|x − y}} < δ}} and {{nowrap|{{abs|f(x) − f(y)}} ≥ ε}}. Therefore, no matter how close we get to any fixed point, there are even closer points at which the function takes not-nearby values.

More general definitions of this kind of function can be obtained, by replacing the absolute value by the distance function in a metric space, or by using the definition of continuity in a topological space.

Dirichlet function

One example of such a function is the indicator function of the rational numbers, also known as the Dirichlet function, named after German mathematician Peter Gustav Lejeune Dirichlet.^[1] This function is denoted as I_Q and has domain and codomain both equal to the real numbers. I_Q(x) equals 1 if x is a rational number and 0 if x is not rational. If we look at this function in the vicinity of some number y, there are two cases:

• If y is rational, then {{nowrap|1=f(y) = 1}}. To show the function is not continuous at y, we need to find an ε such that no matter how small we choose δ, there will be points z within δ of y such that f(z) is not within ε of {{nowrap|1=f(y) = 1}}. In fact, 1/2 is such an ε. Because the irrational numbers are dense in the reals, no matter what δ we choose we can always find an irrational z within δ of y, and {{nowrap|1=f(z) = 0}} is at least 1/2 away from 1.
• If y is irrational, then {{nowrap|1=f(y) = 0}}. Again, we can take {{nowrap|1=ε = 1/2}}, and this time, because the rational numbers are dense in the reals, we can pick z to be a rational number as close to y as is required. Again, {{nowrap|1=f(z) = 1}} is more than 1/2 away from {{nowrap|1=f(y) = 0}}.

In less rigorous terms, between any two irrationals, there is a rational, and vice versa.

The Dirichlet function can be constructed as the double pointwise limit of a sequence of continuous functions, as follows:

for integer j and k.

This shows that the Dirichlet function is a Baire class 2 function. It cannot be a Baire class 1 function because a Baire class 1 function can only be discontinuous on a meagre set.^[2]

In general, if E is any subset of a topological space X such that both E and the complement of E are dense in X, then the real-valued function which takes the value 1 on E and 0 on the complement of E will be nowhere continuous. Functions of this type were originally investigated by Peter Gustav Lejeune Dirichlet.

Hyperreal characterisation

A real function f is nowhere continuous if its natural hyperreal extension has the property that every x is infinitely close to a y such that the difference {{nowrap|f(x) − f(y)}} is appreciable (i.e., not infinitesimal).

See also

• Thomae's function (also known as the popcorn function) — a function that is continuous at all irrational numbers and discontinuous at all rational numbers.
• Weierstrass function: A function continuous everywhere (inside its domain) and differentiable nowhere.

References

External links

• {{springer|title=Dirichlet-function|id=p/d032860}}
• Dirichlet Function — from MathWorld
• The Modified Dirichlet Function by George Beck, The Wolfram Demonstrations Project.

• Wateree people
• Wateree River
• Water efficiency
• Water Efficiency
• Water electrolysis
• Water-electrolyte balance
• Water (Elitsa & Stoyan song)
• Water-elm
• Water elm
• Water empire
• Wateren
• Water erosion
• Water export
• Water exports
• Water extraction device
• Water fairies
• Water fairy
• Water fall
• Waterfall (album)
• Waterfall Bay, Papua New Guinea
• Waterfall Bay (Papua New Guinea)
• Waterfall bong
• Waterfall chart
• Waterfall Cities
• Waterfall CityRail disaster