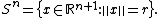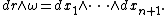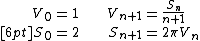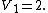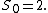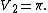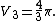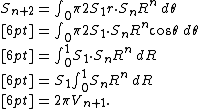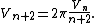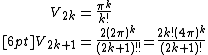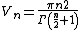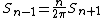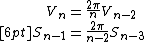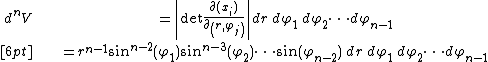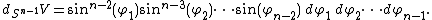“N-sphere”的意思、由来-开放百科全书

In mathematics, the {{math|n}}-sphere is the generalization of the ordinary sphere to spaces of arbitrary dimension. It is an {{math|n}}-dimensional manifold that can be embedded in Euclidean {{math|(n + 1)}}-space.

The 0-sphere is a pair of points, the 1-sphere is a circle, and the 2-sphere is an ordinary sphere. Generally, when embedded in an {{math|(n + 1)}}-dimensional Euclidean space, an {{math|n}}-sphere is the surface or boundary of an {{math|(n + 1)}}-dimensional ball. That is, for any natural number {{math|n}}, an {{math|n}}-sphere of radius {{math|r}} may be defined in terms of an embedding in {{math|(n + 1)}}-dimensional Euclidean space as the set of points that are at distance {{math|r}} from a central point, where the radius {{math|r}} may be any positive real number. Thus, the {{math|n}}-sphere would be defined by:

An n-sphere embedded in an {{math|(n + 1)}}-dimensional Euclidean space is called a hypersphere. The {{math|n}}-sphere of unit radius is called the unit {{math|n}}-sphere, denoted {{math|Sⁿ}}, often referred to as the {{math|n}}-sphere.

When embedded as described, an {{math|n}}-sphere is the surface or boundary of an {{math|(n + 1)}}-dimensional ball. For {{math|n ≥ 2}}, the {{math|n}}-spheres are the simply connected {{math|n}}-dimensional manifolds of constant, positive curvature. The {{math|n}}-spheres admit several other topological descriptions: for example, they can be constructed by gluing two {{math|n}}-dimensional Euclidean spaces together, by identifying the boundary of an {{math|n}}-cube with a point, or (inductively) by forming the suspension of an {{math|(n − 1)}}-sphere.

Description

For any natural number {{math|n}}, an {{math|n}}-sphere of radius {{math|r}} is defined as the set of points in {{math|(n + 1)}}-dimensional Euclidean space that are at distance {{math|r}} from some fixed point {{math|c}}, where {{math|r}} may be any positive real number and where {{math|c}} may be any point in {{math|(n + 1)}}-dimensional space. In particular:

Euclidean coordinates in {{math|(n + 1)}}-space

The set of points in {{math|(n + 1)}}-space, {{math|(x₁, x₂, ..., x_n+1)}}, that define an {{math|n}}-sphere, {{math|Sⁿ}}, is represented by the equation:

where {{math|c}}={{math|(c₁, c₂, ..., c_n+1)}} is a center point, and {{math|r}} is the radius.

The above {{math|n}}-sphere exists in {{math|(n + 1)}}-dimensional Euclidean space and is an example of an {{math|n}}-manifold. The volume form {{math|ω}} of an {{math|n}}-sphere of radius {{math|r}} is given by

where {{math|∗}} is the Hodge star operator; see {{harvtxt|Flanders|1989|loc=§6.1}} for a discussion and proof of this formula in the case {{math|r {{=}} 1}}. As a result,

The space enclosed by an {{math|n}}-sphere is called an {{math|(n + 1)}}-ball. An {{math|(n + 1)}}-ball is closed if it includes the {{math|n}}-sphere, and it is open if it does not include the {{math|n}}-sphere.

Topological description

Topologically, an {{math|n}}-sphere can be constructed as a one-point compactification of {{math|n}}-dimensional Euclidean space. Briefly, the {{math|n}}-sphere can be described as {{math|Sⁿ {{=}} Rⁿ ∪ {∞}}}, which is {{math|n}}-dimensional Euclidean space plus a single point representing infinity in all directions.

In particular, if a single point is removed from an {{math|n}}-sphere, it becomes homeomorphic to {{math|Rⁿ}}. This forms the basis for stereographic projection.^[1]

Volume and surface area

In general, the volume of the {{math|n}}-ball in {{math|n}}-dimensional Euclidean space, and the surface area of the {{math|n}}-sphere in {{math|(n + 1)}}-dimensional Euclidean space, of radius {{math|R}}, are proportional to the {{math|n}}th power of the radius, {{math|R}} (with different constants of proportionality that vary with {{math|n}}). We write {{math|V_n(R) {{=}} V_nRⁿ}} for the volume of the {{math|n}}-ball and {{math|S_n(R) {{=}} S_nRⁿ}} for the surface area of the {{math|n}}-sphere, both of radius {{math|R}}, where {{math|V_n {{=}} V_n(1)}} and {{math|S_n {{=}} S_n(1)}} are the values for the unit-radius case.

Given the radius {{math|R}}, the enclosed volume and the surface area of the {{math|n}}-sphere reach a maximum and then decrease towards zero as the dimension {{math|n}} increases. In particular, the volume {{math|V_n(R)}} enclosed by the {{math|(n – 1)}}-sphere of constant radius {{math|R}} embedded in {{math|n}} dimensions reaches a maximum at the dimension {{math|n}} satisfying {{math|V_n−1 < V_nR}} and {{math|V_n ≥ V_n+1R}} where {{math|V_n}} is given in the sidebar to the right; if the last (weak) inequality holds with equality, then the same maximum also occurs at {{math|n + 1}}. Specifically, for unit radius the largest enclosed volume is that enclosed by a 4-dimensional sphere bounding a 5-dimensional ball.

Similarly, the surface area {{math|S_n(R)}} of the {{mvar|n}}-sphere of constant radius {{mvar|R}} embedded in {{mvar|n + 1}} dimensions reaches a maximum for dimension {{math|n}} that satisfies {{math|S_n−1 < S_nR}} and {{math|S_n ≥ S_n+1R}} where {{math|S_n}} is given in the sidebar to the right; if the last (weak) inequality holds with equality, then the same maximum also occurs at {{math|n + 1}}.^[2] Specifically, for unit radius the largest surface area occurs for the 6-dimensional sphere bounding a 7-dimensional ball.

Examples

The 0-ball consists of a single point. The 0-dimensional Hausdorff measure is the number of points in a set. So,

The unit 1-ball is the interval {{math|[−1,1]}} of length 2. So,

The 0-sphere consists of its two end-points, {{math|{−1,1}}}. So,

The unit 1-sphere is the unit circle in the Euclidean plane, and this has circumference (1-dimensional measure)

The region enclosed by the unit 1-sphere is the 2-ball, or unit disc, and this has area (2-dimensional measure)

Analogously, in 3-dimensional Euclidean space, the surface area (2-dimensional measure) of the unit 2-sphere is given by

and the volume enclosed is the volume (3-dimensional measure) of the unit 3-ball, given by

Recurrences

The surface area, or properly the {{math|n}}-dimensional volume, of the {{math|n}}-sphere at the boundary of the {{math|(n + 1)}}-ball of radius {{math|R}} is related to the volume of the ball by the differential equation

or, equivalently, representing the unit {{math|n}}-ball as a union of concentric {{math|(n − 1)}}-sphere shells,

So,

We can also represent the unit {{math|(n + 2)}}-sphere as a union of tori, each the product of a circle (1-sphere) with an {{math|n}}-sphere. Let {{math|r {{=}} cos θ}} and {{math|r² + R² {{=}} 1}}, so that {{math|R {{=}} sin θ}} and {{math|dR {{=}} cos θ dθ}}. Then,

Since {{math|S₁ {{=}} 2π V₀}}, the equation

holds for all {{math|n}}.

This completes our derivation of the recurrences:

Closed forms

Combining the recurrences, we see that

So it is simple to show by induction on k that,

where {{math|!!}} denotes the double factorial, defined for odd integers {{math|2k + 1}} by {{math|1=(2k + 1)!! = 1 × 3 × 5 ... (2k − 1) × (2k + 1)}}.

In general, the volume, in {{math|n}}-dimensional Euclidean space, of the unit {{math|n}}-ball, is given by

where {{math|Γ}} is the gamma function, which satisfies {{math|Γ({{sfrac|1|2}}) {{=}} {{sqrt|π}}}}, {{math|Γ(1) {{=}} 1}}, and {{math|Γ(x + 1) {{=}} xΓ(x)}}.

By multiplying {{math|V_n}} by {{math|Rⁿ}}, differentiating with respect to {{math|R}}, and then setting {{math|R {{=}} 1}}, we get the closed form

Other relations

The recurrences can be combined to give a "reverse-direction" recurrence relation for surface area, as depicted in the diagram:

Index-shifting {{math|n}} to {{math|n − 2}} then yields the recurrence relations:

where {{math|S₀ {{=}} 2}}, {{math|V₁ {{=}} 2}}, {{math|S₁ {{=}} 2π}} and {{math|V₂ {{=}} π}}.

The recurrence relation for {{math|V_n}} can also be proved via integration with 2-dimensional polar coordinates:

==Spherical coordinates==

We may define a coordinate system in an {{math|n}}-dimensional Euclidean space which is analogous to the spherical coordinate system defined for 3-dimensional Euclidean space, in which the coordinates consist of a radial coordinate {{math|r}}, and {{math|n − 1}} angular coordinates {{math|φ₁, φ₂, ... φ_n−1}}, where the angles {{math|φ₁, φ₂, ... φ_n−2}} range over {{math|[0,π]}} radians (or over {{math|[0,180]}} degrees) and {{math|φ_n−1}} ranges over {{math|[0,2π)}} radians (or over {{math|[0,360)}} degrees). If {{math|x_i}} are the Cartesian coordinates, then we may compute {{math|x₁, ... x_n}} from {{math|r, φ₁, ... φ_n−1}} with: ^[3]

Except in the special cases described below, the inverse transformation is unique:

where if {{math|x_k ≠ 0}} for some {{math|k}} but all of {{math|x_k+1, ... x_n}} are zero then {{math|φ_k {{=}} 0}} when {{math|x_k > 0}}, and {{math|φ_k {{=}} π}} (180 degrees) when {{math|x_k < 0}}.

There are some special cases where the inverse transform is not unique; {{math|φ_k}} for any {{math|k}} will be ambiguous whenever all of {{math|x_k, x_k+1, ... x_n}} are zero; in this case {{math|φ_k}} may be chosen to be zero.

Spherical volume element

Expressing the angular measures in radians, the volume element in {{math|n}}-dimensional Euclidean space will be found from the Jacobian of the transformation:

and the above equation for the volume of the {{math|n}}-ball can be recovered by integrating:

The volume element of the {{math|(n − 1)}}-sphere, which generalizes the area element of the 2-sphere, is given by

The natural choice of an orthogonal basis over the angular coordinates is a product of ultraspherical polynomials,

for {{math|j {{=}} 1, 2,... n − 2}}, and the {{math|e^isφ_j}} for the angle {{math|j {{=}} n − 1}} in concordance with the spherical harmonics.

Stereographic projection

Just as a two-dimensional sphere embedded in three dimensions can be mapped onto a two-dimensional plane by a stereographic projection, an {{math|n}}-sphere can be mapped onto an {{math|n}}-dimensional hyperplane by the {{math|n}}-dimensional version of the stereographic projection. For example, the point {{math|[x,y,z]}} on a two-dimensional sphere of radius 1 maps to the point {{math|[{{sfrac|x|1 − z}},{{sfrac|y|1 − z}}]}} on the {{math|xy}}-plane. In other words,

Likewise, the stereographic projection of an {{math|n}}-sphere {{math|Sⁿ⁻¹}} of radius 1 will map to the {{math|(n − 1)}}-dimensional hyperplane {{math|Rⁿ⁻¹}} perpendicular to the {{math|x_n}}-axis as

Generating random points

Uniformly at random on the {{math|(n − 1)}}-sphere

To generate uniformly distributed random points on the unit {{math|(n − 1)}}-sphere (that is, the surface of the unit {{math|n}}-ball), {{harvtxt|Marsaglia|1972}} gives the following algorithm.

Generate an {{math|n}}-dimensional vector of normal deviates (it suffices to use {{math|N(0, 1)}}, although in fact the choice of the variance is arbitrary), {{math|x {{=}} (x₁, x₂,... x_n)}}. Now calculate the "radius" of this point:

The vector {{math|{{sfrac|1|r}}x}} is uniformly distributed over the surface of the unit {{math|n}}-ball.

An alternative given by Marsaglia is to uniformly randomly select a point {{math|x {{=}} (x₁, x₂,... x_n)}} in the unit {{math|n}}-cube by sampling each {{math|x_i}} independently from the uniform distribution over {{math|(–1,1)}}, computing {{math|r}} as above, and rejecting the point and resampling if {{math|r ≥ 1}} (i.e., if the point is not in the {{math|n}}-ball), and when a point in the ball is obtained scaling it up to the spherical surface by the factor {{math|{{sfrac|1|r}}}}; then again {{math|{{sfrac|1|r}}x}} is uniformly distributed over the surface of the unit {{math|n}}-ball.

Uniformly at random within the {{math|n}}-ball

With a point selected uniformly at random from the surface of the unit {{math|(n - 1)}}-sphere (e.g., by using Marsaglia's algorithm), one needs only a radius to obtain a point uniformly at random from within the unit {{math|n}}-ball. If {{math|u}} is a number generated uniformly at random from the interval {{math|[0, 1]}} and {{math|x}} is a point selected uniformly at random from the unit {{math|(n - 1)}}-sphere, then {{math|u^{{frac|1|n}}x}} is uniformly distributed within the unit {{math|n}}-ball.

Alternatively, points may be sampled uniformly from within the unit {{math|n}}-ball by a reduction from the unit {{math|(n + 1)}}-sphere. In particular, if {{math|(x₁,x₂,...,x_n+2)}} is a point selected uniformly from the unit {{math|(n + 1)}}-sphere, then {{math|(x₁,x₂,...,x_n)}} is uniformly distributed within the unit {{math|n}}-ball (i.e., by simply discarding two coordinates).^[4]

Note that if {{math|n}} is sufficiently large, most of the volume of the {{math|n}}-ball will be contained in the region very close to its surface, so a point selected from that volume will also probably be close to the surface. This is one of the phenomena leading to the so-called curse of dimensionality that arises in some numerical and other applications.

Specific spheres

0-sphere: The pair of points {{math|{±R}}} with the discrete topology for some {{math|R > 0}}. The only sphere that is not path-connected. Has a natural Lie group structure; isomorphic to O(1). Parallelizable.

: //1-sphere">1-sphere : Also known as the circle. Has a nontrivial fundamental group. Abelian Lie group structure U(1); the circle group. Topologically equivalent to the real projective line, RP¹. Parallelizable. SO(2) = U(1).

: //2-sphere">2-sphere : Also known as the sphere. Complex structure; see Riemann sphere. Equivalent to the complex projective line, CP¹. SO(3)/SO(2).

: //3-sphere">3-sphere : Also known as the glome. Parallelizable, Principal U(1)-bundle over the 2-sphere, Lie group structure Sp(1), where also

.

4-sphere: Equivalent to the quaternionic projective line, HP¹. SO(5)/SO(4).

5-sphere: Principal U(1)-bundle over CP². SO(6)/SO(5) = SU(3)/SU(2).

6-sphere: Almost complex structure coming from the set of pure unit octonions. SO(7)/SO(6) = G₂/SU(3). {{See also|6-sphere coordinates}}

7-sphere: Topological quasigroup structure as the set of unit octonions. Principal Sp(1)-bundle over S⁴. Parallelizable. SO(8)/SO(7) = SU(4)/SU(3) = Sp(2)/Sp(1) = Spin(7)/G₂ = Spin(6)/SU(3). The 7-sphere is of particular interest since it was in this dimension that the first exotic spheres were discovered.

8-sphere: Equivalent to the octonionic projective line OP¹.

23-sphere: A highly dense sphere-packing is possible in 24-dimensional space, which is related to the unique qualities of the Leech lattice.

Notes

1. ^James W. Vick (1994). Homology theory, p. 60. Springer
2. ^{{cite journal|last1=Loskot|first1=Pavel|title=On Monotonicity of the Hypersphere Volume and Area|journal=Journal of Geometry|date=November 2007|volume=87|issue=1–2|pages=96–98|doi=10.1007/s00022-007-1891-1}}
3. ^{{cite journal |last1=Blumenson |first1=L. E. |title=A Derivation of n-Dimensional Spherical Coordinates |journal=The American Mathematical Monthly |date=1960 |volume=67 |issue=1 |pages=63–66 |jstor=2308932 |doi=10.2307/2308932 }}
4. ^{{cite report|first1=Aaron R. | last1=Voelker | first2=Jan | last2=Gosmann | first3=Terrence C. | last3=Stewart | title=Efficiently sampling vectors and coordinates from the n-sphere and n-ball | year=2017 | publisher=Centre for Theoretical Neuroscience | url=http://compneuro.uwaterloo.ca/publications/voelker2017.html | doi=10.13140/RG.2.2.15829.01767/1}}

References

{{cite book | last1=Flanders | first1=Harley | title=Differential forms with applications to the physical sciences | publisher=Dover Publications | location=New York | isbn=978-0-486-66169-8 | year=1989|ref=harv}}
{{Cite book | last1=Moura | first1=Eduarda | last2=Henderson | first2=David G. | title=Experiencing geometry: on plane and sphere | url=http://www.math.cornell.edu/~henderson/books/eg00 | publisher=Prentice Hall | isbn=978-0-13-373770-7 | year=1996 | ref=harv | postscript= (Chapter 20: 3-spheres and hyperbolic 3-spaces).}}
{{Cite book | last1=Weeks | first1=Jeffrey R. | author1-link=Jeffrey Weeks (mathematician) | title=The Shape of Space: how to visualize surfaces and three-dimensional manifolds | publisher=Marcel Dekker | isbn=978-0-8247-7437-0 | year=1985 | ref=harv | postscript= (Chapter 14: The Hypersphere).}}
{{cite journal|last=Marsaglia|first=G.|title=Choosing a Point from the Surface of a Sphere|journal=Annals of Mathematical Statistics|volume=43|pages=645–646|year=1972|doi=10.1214/aoms/1177692644|issue=2|ref=harv}}
{{cite journal|first=Greg|last=Huber|title=Gamma function derivation of n-sphere volumes|journal=Amer. Math. Monthly|volume=89|year=1982|pages=301–302|mr=1539933 |jstor=2321716|issue=5|doi=10.2307/2321716|ref=harv

}}

{{cite journal|first1=Nir | last1=Barnea | title=Hyperspherical functions with arbitrary permutational symmetry: Reverse construction

|year=1999 | journal = Phys. Rev. A | doi=10.1103/PhysRevA.59.1135
|volume=59 | number=2|pages=1135–1146}}

External links

[https://web.archive.org/web/20141201023452/http://www.bayarea.net/~kins/thomas_briggs/ Exploring Hyperspace with the Geometric Product]
Properties of Spherical Coordinates in n Dimensions
{{MathWorld|title=Hypersphere|urlname=Hypersphere}}

2 : Multi-dimensional geometry|Spheres