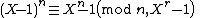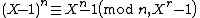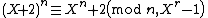- Ramifications
- Truth or falsehood
- Distributed computing
- Notes
- External links
In number theory, Agrawal's conjecture, due to Manindra Agrawal in 2002,[1] forms the basis for the cyclotomic AKS test. Agrawal's conjecture states formally:
Let 
and 
be two coprime positive integers. If
then either is prime or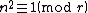 
Ramifications
If Agrawal's conjecture were true, it would decrease the runtime complexity of the AKS primality test from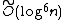 
to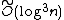 
.
Truth or falsehood
The conjecture was formulated by Rajat Bhattacharjee and Prashant Pandey in their 2001 thesis.[2] It has been computationally verified for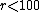 
and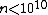 
,[3] and for 
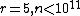.[4]
However, a heuristic argument by Carl Pomerance and Hendrik W. Lenstra suggests there are infinitely many counterexamples.[5] In particular, the heuristic shows that such counterexamples have asymptotic density greater than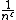 
for any 
.
Assuming Agrawal's conjecture is false by the above argument, Roman B. Popovych conjectures a modified version may still be true:
Let and be two coprime positive integers. If
and
then either is prime or 
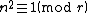.[6]
Distributed computing
Both Agrawal's conjecture and Popovych's conjecture are being tested by distributed computing project Primaboinca, which was started in 2010 based on BOINC. As of June 2017, the project found no counterexample for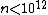 
.
Notes
2. ^{{cite journal|author=Rajat Bhattacharjee, Prashant Pandey|date=April 2001|url=https://cs.stanford.edu/people/rajatb/primality.ps.gz |title=Primality Testing|journal=Technical report|publisher=IIT Kanpur}}
3. ^{{cite journal|author=Neeraj Kayal, Nitin Saxena|year=2002|title=Towards a deterministic polynomial-time Primality Test|journal=Technical report|publisher=IIT Kanpur|url=http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=26D074BAD51A77850596AC6713BBC741?doi=10.1.1.16.9281&rep=rep1&type=pdf}}
4. ^{{cite web|url=https://www.cse.iitk.ac.in/users/nitin/talks/Dec2014-3Paris.pdf|title=Primality & Prime Number Generation|last=Saxena|first=Nitin|date=Dec 2014|publisher=UPMC Paris|accessdate=24 April 2018}}
5. ^{{cite web|last=Lenstra|first=H. W.|first2=Carl|last2=Pomerance|date=2003|title=Remarks on Agrawal’s conjecture.|url=http://www.aimath.org/WWN/primesinp/primesinp.pdf|publisher=American Institute of Mathematics|accessdate=16 October 2013}}
6. ^{{citation|url=https://eprint.iacr.org/2009/008.pdf |title=A note on Agrawal conjecture |first=Roman |last=Popovych|date=30 December 2008|accessdate=21 April 2018}}
External links
- Primaboinca project
- List of Justice awards and nominations
- List of Justice Ministers of France
- List of Justice Ministers of Imperial Russia
- List of Justices in the Supreme Court of Norway
- List of Justices of Islamabad High Court
- List of justices of islamabad high cout
- List of Justices of Supreme Court of Pakistan
- List of Justices of the Alabama Supreme Court
- List of justices of the Alabama Supreme Court
- List of Justices of the Alaska Supreme Court
- List of justices of the Alaska Supreme Court
- List of Justices of the Arizona Supreme Court
- List of justices of the Arizona Supreme Court
- List of justices of the Arkansas Supreme Court
- List of Justices of the Arkansas Supreme Court
- List of justices of the California Supreme Court
- List of Justices of the California Supreme Court
- List of justices of the Colorado Supreme Court
- List of Justices of the Colorado Supreme Court
- List of justices of the Connecticut Supreme Court
- List of Justices of the Connecticut Supreme Court
- List of Justices of the Court of Common Pleas
- List of justices of the Florida Supreme Court
- List of Justices of the Florida Supreme Court
- List of Justices of the Hawaii Supreme Court