- Description and basic concepts
- See also
- References
- Further reading
In mathematics, the Almgren–Pitts min-max theory (named after Frederick J. Almgren, Jr. and his student Jon T. Pitts) is an analogue of Morse theory for hypersurfaces.
The theory started with the efforts for generalizing George David Birkhoff's method for the construction of simple closed geodesics on the sphere, to allow the construction of embedded minimal surfaces in arbitrary 3-manifolds.[1]
It has played roles in the solutions to a number of conjectures in geometry and topology found by Almgren and Pitts themselves and also by other mathematicians, such as Mikhail Gromov, Richard Schoen, Shing-Tung Yau, Fernando Codá Marques, André Neves, Ian Agol, among others.[2][3][4][5][6][7][8][9][10]
Description and basic concepts
{{expand section|date=May 2015}}The theory allows the construction of embedded minimal hypersurfaces though variational methods.[11]
See also
- Varifold
- Geometric measure theory
- Geometric analysis
- Minimal surface
- Freedman–He–Wang conjecture
- Willmore conjecture
- Yau's conjecture
References
2. ^{{cite web |url=http://numdam.mathdoc.fr/numdam-bin/item?id=ASNSP_2006_5_5_4_483_0 |author1=Giaquinta, Mariano |author2=Mucci, Domenico |title=The BV-energy of maps into a manifold : relaxation and density results |publisher=Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Sér. 5, 5|number=4 |date=2006 |pages=483–548}}
3. ^Helge Holden, Ragni Piene – The Abel Prize 2008-2012, p. 203.
4. ^Robert Osserman – A Survey of Minimal Surfaces, p. 160.
5. ^{{cite web |url=http://intlpress.com/site/pub/pages/journals/items/cdm/content/vols/2013/0001/a001/index.html |title=Content Online - CDM 2013 Article 1 |publisher=Intlpress.com |accessdate=2015-05-31}}
6. ^{{cite web |url=http://wwwf.imperial.ac.uk/~aneves/papers/CDM-harvard3.pdf |format=PDF |title=Applications of Almgren-Pitts Min-max theory |author1=Fernando C. Marques |author2=André Neves |publisher=F.imperial.ac.uk |accessdate=2015-05-31}}
7. ^{{Cite arXiv |title=Degeneration of Min-Max Sequences in Three-Manifolds |author1=Daniel Ketover |arxiv=1312.2666}}
8. ^{{cite web |url=http://xxx.tau.ac.il/pdf/1504.00966.pdf |format=PDF |title=Min-max hypersurface in manifold of positive Ricci curvature |author=Xin Zhou |publisher=Arvix.org |accessdate=2015-05-31}}
9. ^{{cite web|url=http://perso-math.univ-mlv.fr/users/sabourau.stephane/articles/hypersurface.pdf |format=PDF |title=Volume of minimal hypersurfaces in manifolds with nonnegative Ricci curvature |author=Stephane Sabourau |publisher=Arvix.org |accessdate=2015-05-31}}
10. ^{{Cite arXiv|title=Free boundary minimal annuli in convex three-manifolds |author1=Davi Maximo |author2=Ivaldo Nunes |author3=Graham Smith |arxiv=1312.5392 }}
11. ^{{cite journal | author = Zhou Xin | year = 2015 | title = Min-max minimal hypersurface in
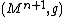 with
with 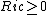 and
and 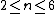 | url = http://projecteuclid.org/euclid.jdg/1427202766 | journal = J. Differential Geom. | volume = 100 | issue = 1 | pages = 129–160 | doi=10.4310/jdg/1427202766}}
| url = http://projecteuclid.org/euclid.jdg/1427202766 | journal = J. Differential Geom. | volume = 100 | issue = 1 | pages = 129–160 | doi=10.4310/jdg/1427202766}}Further reading
- {{cite book |author=Frederick J. Almgren |title=The Theory of Varifolds: A Variational Calculus in the Large for the K-dimensional Area Integrand |date=1964 |publisher=Institute for Advanced Study}}
- {{cite book |author=Jon T. Pitts|title=Existence and Regularity of Minimal Surfaces on Riemannian Manifolds |date=1981 |publisher=Princeton University Press |isbn=978-0-691-08290-5}}
- {{Cite arXiv |arxiv=1312.0792 |last1=Memarian |first1=Yashar |title=A Note on the Geometry of Positively-Curved Riemannian Manifolds |class=math.MG |date=2013 }}
- Le Centre de recherches mathématiques, CRM Le Bulletin, Automne/Fall 2015 — Volume 21, No 2, pp. 10–11 Iosif Polterovich (Montréal) and Alina Stancu (Concordia), "The 2015 Nirenberg Lectures in Geometric Analysis: Min-Max Theory and Geometry, by André Neves"
- Marine Environmental Protection (USCG)
- Marine, Estuarine, & Environmental Sciences
- Marine Explorer
- Marine Facade
- Marinefahrprahm
- Marinefahrpram
- Marine Farms
- Marine F C
- Marine F. C.
- Marine Fighter Attack Squadron 451
- Marine Fighter Attack Training Squadron 501
- Marine Fighting Squadron 132
- Marine Fighting Squadron 212
- Marine Fighting Squadron 215
- Marine Fighting Squadron 218
- Marine Fighting Squadron 222
- Marine Fighting Squadron 236
- Marine Fighting Squadron 413
- Marine Fighting Squadron 441
- Marine Fighting Squadron 452
- Marine Fighting Squadron 511
- Marine firefighting
- Marineflieger
- Marine floor
- Marine force