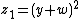“Analytically irreducible ring”的意思、由来-开放百科全书

词条

Analytically irreducible ring

释义

Nagata's example
References

In algebra, an analytically irreducible ring is a local ring whose completion has no zero divisors. Geometrically this corresponds to a variety with only one analytic branch at a point.

{{harvtxt|Zariski|1948}} proved that if a local ring of an algebraic variety is a normal ring, then it is analytically irreducible. There are many examples of reduced and irreducible local rings that are analytically reducible, such as the local ring of a node of an irreducible curve, but it is hard to find examples that are also normal. {{harvs|txt|last=Nagata|year1=1958|year2=1962|loc2=Appendix A1, example 7}} gave such an example of a normal Noetherian local ring that is analytically reducible.

Nagata's example

Suppose that K is a field of characteristic not 2, and K {{brackets|x,y}} is the formal power series ring over K in 2 variables. Let R be the subring of K {{brackets|x,y}} generated by x, y, and the elements z_n and localized at these elements, where

is transcendental over K(x)

.

Then R[X]/(X²–z₁) is a normal Noetherian local ring that is analytically reducible.

References

{{citation|mr=0097395|last=Nagata|first= Masayoshi|title=An example of a normal local ring which is analytically reducible|journal=Mem. Coll. Sci. Univ. Kyoto. Ser. A. Math.|volume= 31|year= 1958|pages= 83–85|url= http://projecteuclid.org/euclid.kjm/1250776950}}
{{citation|authorlink=Masayoshi Nagata|last=Nagata|first= Masayoshi|title=Local rings|series= Interscience Tracts in Pure and Applied Mathematics|volume= 13|publisher= Interscience Publishers|place=New York-London |year=1962}}
{{citation| mr=0024158 |last=Zariski|first= Oscar|authorlink=Oscar Zariski|title=Analytical irreducibility of normal varieties|journal=Ann. of Math. |series= 2 |volume=49|year=1948|pages= 352–361|doi=10.2307/1969284}}
{{Citation | last1=Zariski | first1=Oscar | author1-link=Oscar Zariski | last2=Samuel | first2=Pierre | author2-link=Pierre Samuel | title=Commutative algebra. Vol. II | origyear=1960 | publisher=Springer-Verlag | location=Berlin, New York | isbn=978-0-387-90171-8 |mr=0389876 | year=1975}}

1 : Commutative algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。